|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
PCA算法是属于SVD算法的一种,叫做Principal Component Analysis,是用于数据压缩用的。在真实情况下我们处理的数据都是相当大的,几亿甚至几十亿,数据的维度有上千维(就是上千个矩阵的列)。电脑处理起来非常慢,就需要降维。我们以MINIST数据为例介绍一下PCA算法,先把以前的代码复制过来(你的电脑目录下最好之前已经下载了MINIST数据集):
- from sklearn.datasets import fetch_mldata
- import numpy as np
- mnist=fetch_mldata('MNIST original',data_home='.\datasets\mldata')
- X,y=mnist["data"],mnist["target"]
- %matplotlib inline
- import matplotlib
- import matplotlib.pyplot as plt
- some_digit=X[36000]
- some_digit_imge=some_digit.reshape(28,28)
- plt.imshow(some_digit_imge,cmap=matplotlib.cm.binary,interpolation="nearest")
- plt.axis("off")
- plt.show()
输出的这张图是一个数字5,下面我们将所有的数据进行压缩:
- from sklearn.decomposition import PCA
- pca=PCA(n_components=144)
- X_minist_reduced=pca.fit_transform(X)
- X_minist_recovered=pca.inverse_transform(X_minist_reduced)
然后再画图:
- some_digit=X_minist_reduced[36000]
- some_digit_imge=some_digit.reshape(12,12)
- plt.imshow(some_digit_imge,cmap=matplotlib.cm.binary,interpolation="nearest")
- plt.axis("off")
- plt.show()
输出的这张图片是一张非常模糊的图片,如下:

原来是28*28的矩阵被我们压缩为14*14了,但是特征还是存在这张图片里,只是我们肉眼没法分辨而已,下面我们看看还原后的图片(以上代码里的第二个变量X_minist_recovered就是还原的数据):
- some_digit=X_minist_recovered[36000]
- some_digit_imge=some_digit.reshape(28,28)
- plt.imshow(some_digit_imge,cmap=matplotlib.cm.binary,interpolation="nearest")
- plt.axis("off")
- plt.show()
输出图片为:
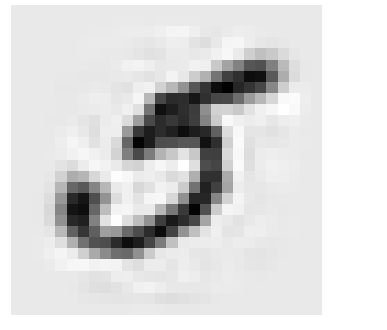
比原图稍微有点模糊,因为这个压缩会有些误差的,叫做reconstruction error。
如果我们进行大数据量的压缩,电脑没办法一次读取到内存中,就要使用以下方法进行压缩:
- from sklearn.decomposition import IncrementalPCA
- n_batches=100
- inc_pca=IncrementalPCA(n_components=144)
- for X_batch in np.array_split(X,n_batches):
- inc_pca.partial_fit(X_batch)
- X_minist_reduced=inc_pca.transform(X)
然后画图:
- some_digit=X_minist_reduced[36000]
- some_digit_imge=some_digit.reshape(12,12)
- plt.imshow(some_digit_imge,cmap=matplotlib.cm.binary,interpolation="nearest")
- plt.axis("off")
- plt.show()
输出图片为:
就跟上次的压缩效果一样。还有一种随机的压缩方式速度会快点:
- rnd_pac=PCA(n_components=144,svd_solver="randomized")
- X_reduced=rnd_pac.fit_transform(X)
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)