最大质因数算法优化

ietar

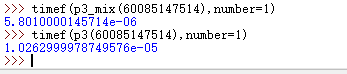
p3为原算法 p3_mix为优化后算法 开头的timef为手写计时小轮子

原算法思路 从小到大取约数n 尝试整除原数a 整除成功则令a=a/n 循环直到a为质数 此时a为原数的最大质因数

p3_mix 优化了取余数的过程 记录上次取到的余数n 每次循环从n开始从小到大取约数 并只取质数（合数均可表示为质数乘积）

p3_get_prime(n)只简单用了质数的通项公式 并未对n进行检测 因此返回值中带有不合要求的合数 好在也含有全部质数 就是每一跳步子不够大

(哪怕来个质数的迭代公式也好啊)


在一些情况下 mix算法效率明显高于原算法
比如 60085147514 （原题600851475143 去掉了最后的3）

half_failed_fix

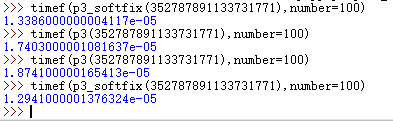
取约数时保存上次循环进度 不考虑质数的p3_softfix()

soft_fix

import time

def timef(function,number=1000):
        t1=time.perf_counter()
        for i in range(number):
                function
        t2=time.perf_counter()
        return t2-t1

def p3(a = 600851475143):
    import math 
    def p3_get_prime(n):
        return int(3*n+1+(math.sin(math.pi*n/2))**2)

    def is_prime(n):
        if not n%2:
            return False
        n1 = int(math.sqrt(n))
        for i in range(3,n1+1,2):
            if not n%i:
                return False
        return True
    
    # 肉眼可见2不是a的约数
    def p3_1(n,num=1):
        if is_prime(n):
            return n
        for i in range(3,a//3+1):
            if not n%i:
                return p3_1(n/i)
    return (p3_1(a))
    
def p3_softfix(a = 600851475143):
    import math 
    def p3_get_prime(n):
        return int(3*n+1+(math.sin(math.pi*n/2))**2)

    def is_prime(n):
        if not n%2:
            return False
        n1 = int(math.sqrt(n))
        for i in range(3,n1+1,2):
            if not n%i:
                return False
        return True
    
    # 肉眼可见2不是a的约数
    def p3_1(n,num=2):
        if is_prime(n):
            return n
        for i in range(num,int(n//3)+1):
            if not n%i:
                num = i
                return p3_1(n/i,num)
    return p3_1(a)


def p3_mix(a = 600851475143):
    import math 
    def p3_get_prime(n):
        #产生的并不仅是质数 但包含所有质数 just ok
        return int(3*n+1+(math.sin(math.pi*n/2))**2)

    def is_prime(n):
        if not n%2:
            return False
        n1 = int(math.sqrt(n))
        for i in range(3,int(n//3)+1):
            if not n%i:
                return False
        return True
    
    def p3_1_mix(n,num=1,i=2):
        if is_prime(n):
            return n
        while i < n//2+1:
            if not n%i:  # n被i整除
                return p3_1_mix(n/i,num,i)
            else:  # n无法被i整除
                if i == 2:
                    i = 3
                elif i == 3:
                    i = p3_get_prime(num)
                else:
                    num += 1
                    i=p3_get_prime(num)
    return (p3_1_mix(a))