计算机程序设计常用方法“起死回生” 初章 基本篇 第一篇 递归方法

沉默的人e

                               
登录/注册后可看大图

沉默的人e

                                        初章-基本篇

第一篇递归方法

这应该是最初见到的方法。

好了问题来了。什么是递归？

之前在小甲鱼论坛里发了个帖子，叫“我看递归”。结果发现效果很差，懂了的人懂了，没懂的人依然没懂。

递归分为两步，首先是“递”，就是递推，如果大家学过数列的话，数列里除了通项公式，还有一种叫“递推公式”对吧。

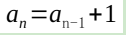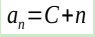
这里的递推就是这个意思。在数列里，递推公式就是像 的公式。通过这个递推公式也很容易知道，通项公式是 。好巧不巧的是，这里为什么会多出来一个C？这就是递推的结果，由于不知道最下面一层返回了什么，所以不能确定最终结果是什么。所以才会出现这么一个C。

为了解决这个C的问题，就需要用到回归。告诉这个公式，最底下一层是什么。于是完美的递归公式，就应该是这样的：

n的值由用户来决定，而且上面的公式由于都是a下的法则，所以对于n-1也可以按照上面的公式进行处理，一层一层的，一直到n= 1 的时候。对n= 1 进行特殊处理（第二个公式）以后，层层返回。

这个例子如果没有让诸位同胞们开窍，我再举几个。

比如，写出等差数列求和的函数（递归方法）。

同样的，先写出递推内容,暂时让公差为1。思考一下过程。比如我让它从上往下加，从最大的往下加。每一次都加的是比这个数小一的数。假设次数为x，那么加的过程是：x+ x-1 + x-1-1 + x-1-1-1+...，对吧。现在给这个东西压上括号：x+ (x-1 + (x-1-1 +(x-1-1-1+(...))))。每一层都只保留一个待知数x，从数学公式上也行的通。现在分析这个带括号的东西，x加上一个整体，这个整体把x-1扔出去，然后将剩下的部分再作为整体，同样的下面的整体把x-1-1扔出去，剩下的作为整体……

我们惊奇的发现，除了值有那么一丢丢的偏差，从形式上看，完全相同。现在思考形式，每一次都是单独的变量被扔出去，然后加一个整体，整体中也在进行着同样的操作，所以他们按照同样的对应法则处理数据。假设这个法则是f,那么很简单的，我们可以得到这个公式

我说了，这只是递推.没有回归，要想回归，要明白在最底层时应该是什么。举个例子，我令最底层为1，也就是说f(1)= 1。整合起来公式应该这么写：

稍微思考，就可以知道，这是求1+2+3+...+100的和。

沉默的人e

再举一个例子，汉诺塔。这个例子被很多老师用，因为太经典了。

规则不说了。假设第一个柱上有n个片片，三个柱子叫a,b,c

每次移动的方式都是相同的，起个名字叫做hanoi方法。要将n个片片从a通过b移动到c。移动的方法是将在最上面的n-1个片片通过b移动到c，将a上的最下面的片片移动到c。同样的道理，b上的所有片片也是执行这样的hanoi方法移动到c上就可以了。因为每一次的移动都是按照这个hanoi方法，变的仅仅是你的片片的数，而从a移动到c要保留最下面的片片，所以从b移动到c上的时候片片数n变成了n-1。

hanoi方法写成算法是这样的：

第一步，利用hanoi方法（递推）将a上的(n-1)个片片移动到b上；（把第二步视为最底层）

第二步，将最后一个片片移动到c上（这里是回归）

第三步，将b上的(n-1)个片片利用hanoi方法移动到c上。（这里又是递推,第二步可以视为是递推的最底层）

使用递归的前提条件是，每一层运用的方法都是相同的，如果不相同，当然不能运用递推回归方法。更重要的是，你写的函数如果有递推，就一定要有回归。

这就是我对递归的理解，上面的几个例子希望能对个位鱼友有所帮助。如果仍有什么没说清楚的，请各位在下方留言。