|
|
20鱼币
本帖最后由 dequantianhe 于 2019-12-29 14:27 编辑
各位大佬,今日老弟习题做到S1E36:快速排序 的马踏棋盘问题,经过苦思冥想自认为找到了解决的思路,但代码写完,程序跑起来,最多运行七八个小时,已然没有一个结果得出。
于是我感觉是我的逻辑有问题,但自己反复查看又找不到问题,而这个程序实现所需要的运算量极大,又不可能实际手动去校正(实际我经过了简单的尝试,也未发现问题)。
故烦请各位大佬上演看看,问题究竟在哪里!
上代码前,先简单的说一下我的思路:
整体思路:一个8*8的棋盘一共64位,最后的结果就是要按照马走日的行进方式对64位进行排序,能全部排出来就是正确结果。
1、棋盘64位小弟首先对他们进行编号,按照0~63的顺序,生命为全局变量qipannum[2],qipannum[0]是本位的编号,qipannum[1]的值只有0/1两种值,0代表尚未排序,1代表已排序。
2、先通过条件计算出每一位通过马走日的规矩可以指向的下一位的编号,得到64*8的一个数组mybe。(64个编号,最多8种可能)
3、声明变量deep,即每次遍历中已排序的棋盘位数(从0开始到63结束);
4、定义一个全局变量result[1000][64],用来存放每次遍历成功的结果。
5、声明一个64位数组test,用来存放每次已排序的棋盘位数,等test填满,deep值为63时排序成功,将test此时的值传给result[count],count值从0开始,代表总共得到多少种答案了。
6、最关键的遍历部分,从主函数中用for循环依次给test[0]赋初值(0~63),利用初值带入真正的循环函数calcu()
7、函数calcu的逻辑定义:
a、先判断deep值是否为63,是的话说明排序已完成,赋值给result后返回。
b、deep值小于63,说明排序未完成,需要进行以下操作:
利用最新以排序的值p[deep],去遍历这个值在mybe中有多少种可以安排的下一位,下一位next要求值大于等于0,且下一位的值在棋盘qipannum[next ][1]的对应值不为1(即尚未被安排)
找到符合条件的next后,把第一个符合条件的next排序,赋值给p[deep+1],同时设定qipannum[next][1]的值为1,即标记为已排序。
再次调用自己,将新的deep值代入,如此循环遍历,直到没有合适的next后,返回,内层calcu函数执行完毕后,要设置qipannum[next ][1]的值为0,即准备下一次循环。
8、整个程序还是一个循环遍历的思路,直到把所有可能的组合全部遍历完毕,得到所有的可能的答案。
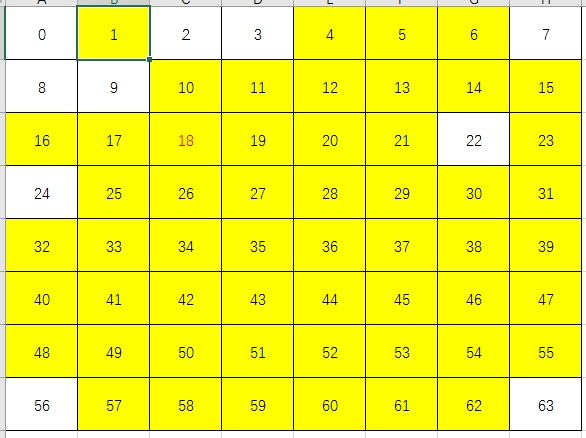
qipannum编号示意图(横向为x,纵向为y):
下面把代码打一下:(部分细节还可以优化,暂且先这样)
#include<stdio.h>
int qipanxy[64][2];
int qipannum[64][2];
int result[1000][64];
void getpossible(int p[2], int q[8]);
void getpossible(int p[2], int q[8])
{
int i;
q[0]=8>p[1]+1 && p[1]+1 >= 0 && 8>p[0] +2 && p[0]+2>=0?(p[1]+1)*8+p[0]+2:-1;
q[1]=8>p[1]+1 && p[1]+1 >= 0 && 8>p[0] - 2 && p[0]- 2>=0?(p[1]+1)*8+p[0]+2:-1;
q[2]=8>p[1]- 1 && p[1]- 1 >= 0 && 8>p[0] +2 && p[0]+2>=0?(p[1]- 1)*8+p[0]+2:-1;
q[3]=8>p[1]- 1 && p[1]- 1 >= 0 && 8>p[0] - 2 && p[0]- 2>=0?(p[1]- 1)*8+p[0]+2:-1;
q[4]=8>p[1]+2 && p[1]+2 >= 0 && 8>p[0] +1 && p[0]+1>=0?(p[1]+2)*8+p[0]+2:-1;
q[5]=8>p[1]+2 && p[1]+2 >= 0 && 8>p[0] - 1 && p[0]- 1>=0?(p[1]+2)*8+p[0]+2:-1;
q[6]=8>p[1]- 2 && p[1]- 2 >= 0 && 8>p[0] +1 && p[0]+1>=0?(p[1]- 2)*8+p[0]+2:-1;
q[7]=8>p[1]- 2 && p[1]- 2 >= 0 && 8>p[0] - 1 && p[0]- 1>=0?(p[1]- 2)*8+p[0]+2:-1;
for(i = 0;i <8;i++)
{
if(q[i]< 0||q[i]>63)
{
q[i] = -1;
}
}
}
int calcu(int p[64], int q[64][8], int *count, int deep);
int calcu(int p[64], int q[64][8], int *count, int deep)
{
int i,j,tmp,k;
if(deep == 63)
{
for(k=0;k < 64;k++)
{
result[*count][k] = p[k];
}
(*count)++;
printf("sucessfully!");
return;
}
else
{
for(j = 0; j< 8; j++)//开始遍历p[deep]数值可能对应的下一步的所有数值
{
tmp = q[p[deep]][j];
if(tmp >= 0 && qipannum[tmp][1] != 1)
{
p[deep+1]= tmp;//增加新的排序数值
qipannum[tmp][1]=1;//标记为已排序
calcu(p,q,count,deep+1);//调用自身,进行下一层排序判断
qipannum[tmp][1]=0;//第deep+1层排序为tmp的可能性已遍历完,解除标记,为第deep+1层为下个可能的数值做准备。
}
}
}
}
int main(void)
{
int mybe[64][8];
int i,j,count = 0;
int *p = &count;
int test[64] = {-2};
for(i = 0; i< 8;i++)
{
for(j = 0; j< 8; j++)
{
qipanxy[i*8+j][0]= j;//j为x
qipanxy[i*8+j][1]= i;//i为y
qipannum[i*8+j][0]= i*8+j; //给qipannum赋值,这一步可能没啥必要,但不影响结果
qipannum[i*8+j][1]= 0;
}
}
for(i = 0;i< 64;i++)
{
getpossible(qipanxy[i],mybe[i]);
}
for(i = 0;i< 64; i++)//将mybe的结果打出
{
printf("%d对应的可能下一步的数字:",i)
for(j = 0;j< 8;j++)
{
printf("%d ",mybe[i][j]);
}
printf("\n");
}
for(i = 16;i< 64;i++)//i应该从0开始遍历,但小甲鱼说从16开始容易得到结果,可惜我这里尝试后还是没有结果
{
test[0] = i;
qipannum[i][1]= 1;
calcu(test,mybe,p,0);
qipannum[i][1] = 0;
}
for(i = 0; i< count; i++)
{
printf("第%d种行走方案:",i);
for(j = 0;j< 64;j++)
{
printf("%d ",result[i][j]);
}
printf("\n");
}
return 0;
}
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)