|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
本帖最后由 zltzlt 于 2020-2-24 21:24 编辑
C++ 树的基本概念
树的定义
树是由 n 个节点构成的有限集合。
当 n 等于 0 时,树称为空树;
当 n 不等于 0 时,树中的节点应该满足以下两个条件:
- 有且仅有的一个特定的结点称之为根;
- 其余结点分成 m 个互不相交的有限集合 T1, T2, ......., Tm,其中每个集合又是一棵树,称 T1, T2, ......., Tm 结点为根结点的子树。
注:树的定义具有递归性,即树里还有子树。
树的图示
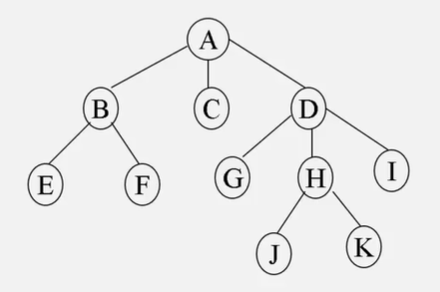
双亲、子女与兄弟
在树中采用线段连接两个相关联的结点,如下图中的 D 和 H 。
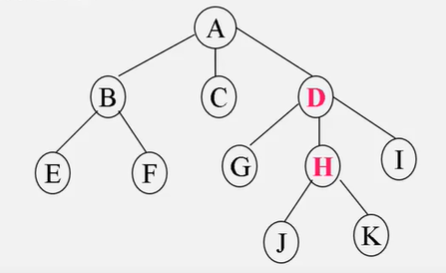
其中 D 是上端结点,H 是下端结点。称 D 是 H 的双亲(也称父母或前件),H 为 D 的子女(也称孩子或后件)。
双亲和子女的关系是相对而言的。图中,B 是 A 的子女,但 B 又是 E 和 F 的双亲。
由于 E 和 F 的双亲为同一结点 B,因此称 E 和 F 互为兄弟。
在任何一棵树中,除根结点外,其他任何一个结点有且仅有一个双亲,有 0 个或多个子女,且它的子女恰巧为其子树的根结点。
结点的度与树的度
将一个节点拥有的子女数称之为该结点的度,树中所有结点度的最大值称为树的度。
在这棵树中,A 的度为 3,B 的度为 2,而 C 的度为 0,整棵树的度为 3。
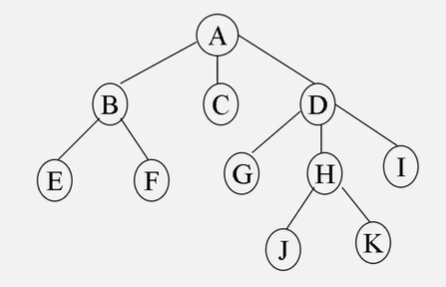
叶子结点与分支结点
度为 0 的结点为叶子结点(或终端结点),度不为 0 的结点为分支结点(或非终端结点)。
在这棵树中,A、B、D、H 均为分支结点,而 E、F、C、G、J、K、I 均为叶子结点。
树枝与路径
树中连接两个结点的线段为树枝。
在树中,若从结点 Ki 开始,沿着树枝自上而下能到达结点 Kj,则称从 Ki 到 Kj 存在一条路径,路径的长度等于所经过的树枝的条数。
在下面这棵树中,从 A 到 J 存在一条长度为 3 的路径,从 D 和 K 也存在一条长度为 2 的路径。
结点的层次与树的深度
树中结点的层次:从树根开始定义,根结点为第一层,根的子女结点构成第二层,以此类推。
树中结点的最大层次数为树的深度。
例如下面这棵树的高度为 4 。
有序树和无序树
若树中任意结点的子树均看成是从左到右有次序的,不能随意交换,则称该树为有序树;否则称该树为无序树。
森林
由 m 棵互不相交的树构成的集合称为森林。[/b] |
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)