Leetcode 987. Vertical Order Traversal of a Binary Tree

Seawolf

Given a binary tree, return the vertical order traversal of its nodes values.

For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).

Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).

If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.

Return an list of non-empty reports in order of X coordinate.  Every report will have a list of values of nodes.

 

Example 1:









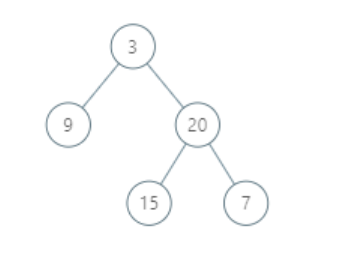
Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation: 
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).
Example 2:









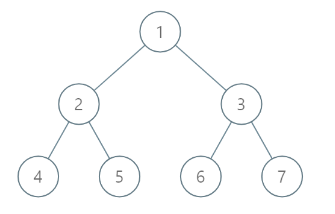
Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation: 
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.
 

Note:

The tree will have between 1 and 1000 nodes.
Each node's value will be between 0 and 1000.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def verticalTraversal(self, root: TreeNode) -> List[List[int]]:
        res = []
        if root == None:
            return res
        hashmap = collections.defaultdict(list)
        queue = []
        cols = []
        max_val = 0
        min_val = 0
        level = 0
        queue.append(root)
        cols.append(0)
        
        while queue:
            size = len(queue)
            for i in range(size):
                curt = queue.pop(0)
                col = cols.pop(0)
                hashmap[col].append((level, curt.val))
                if curt.left != None:
                    min_val = min(min_val, col - 1)
                    queue.append(curt.left)
                    cols.append(col - 1)
                if curt.right != None:
                    max_val = max(max_val, col + 1)
                    queue.append(curt.right)
                    cols.append(col + 1)
            level += 1
        
        for i in range(min_val, max_val + 1):
            res.append([j for i, j in sorted(hashmap[i])])
        return res