[已解决]C语言 最近对问题

William_Prince

下面是题目和测试用例


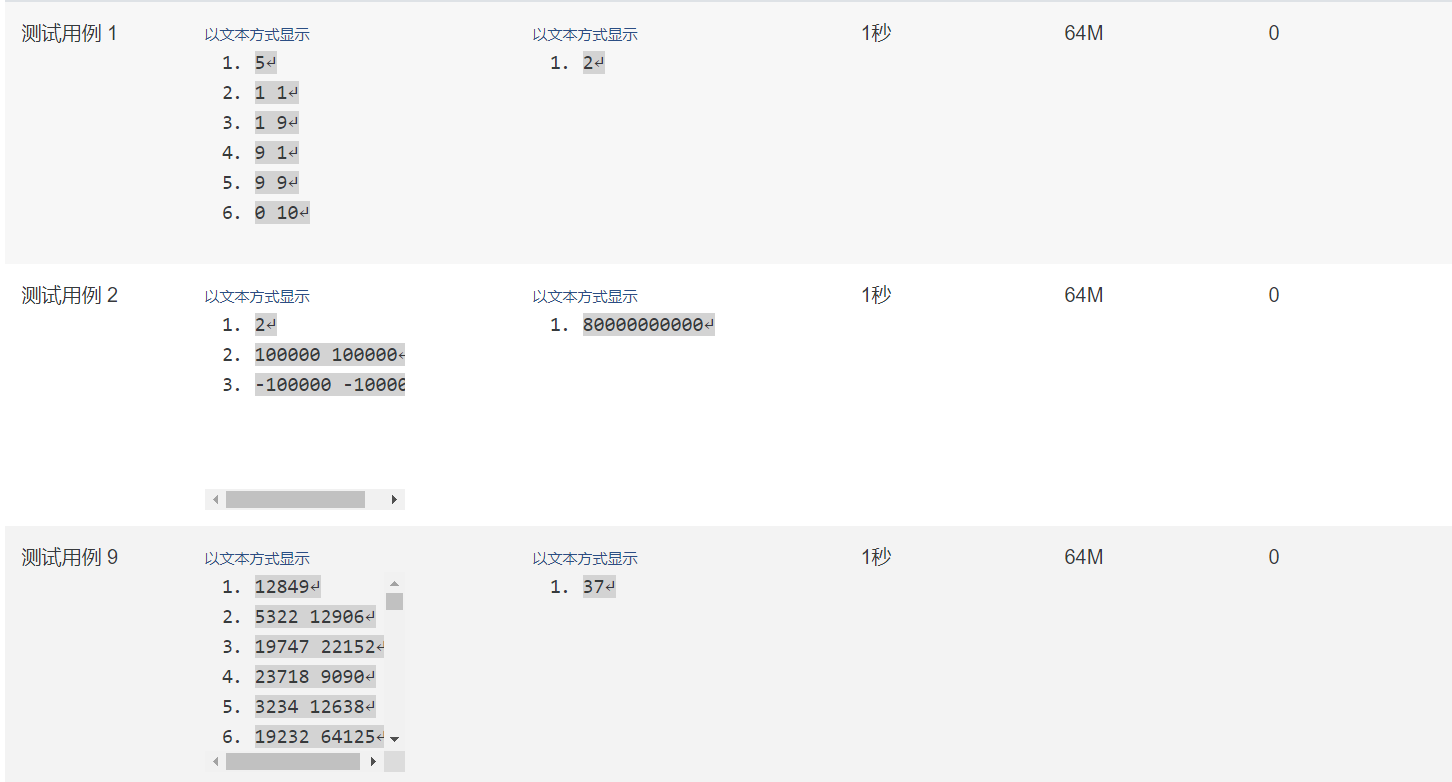
以下是我的代码

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>

#define INF 2147483647
#define N 1000000

struct node{
        int x;
        int y;
}point[N];

int cmp(const void *a,const void *b)
{
        struct node ac = *(struct node*)a;
        struct node bd = *(struct node*)b;
        if (ac.x != bd.x) 
                return ac.x - bd.x;
        else return ac.y - bd.y;
}//结构体排序 


int mindistance(int left,int right){
        return left<right?left:right;//返回大小关系 
}

int distance(int left,int right){
        return ((point[left].x - point[right].x)*(point[left].x - point[right].x) + (point[left].y - point[right].y)*(point[left].y - point[right].y));
}//计算距离的平方 

int Closest_Pair(int left,int right){
        int End_dis = INF;
        int i=0,j=0,k=0;
        
        if (left == right) return End_dis;//假如区间里面只有一个点，那么返回无穷大 
        if (right - left == 1) return distance(left,right);//假如区间里面只有两个点，那么直接返回这两点之间距离的平方
         
        
        int mid = (left + right)/2;//计算中线，判断是否是大于等于三个点的情况
        
        int distanceleft  = Closest_Pair(left,mid);//左边递归 
        int distanceright = Closest_Pair(mid+1,right);//右边递归
        
        End_dis = mindistance(distanceleft,distanceright) ;//比较左右两边距离的平方，找出最小值，即为d 
        
        int temp[N] = {0}; //储存宽度为d的点
        
        for (i = left; i < right; i++){//找出符合要求的距离mid横坐标的平方小于d的点 
                if ( (point[left].x - point[right].x)*(point[left].x - point[right].x) <= End_dis ){
                        temp[k++] = i;//temp用来暂时存储符合要求的点的序号 
                }
        } 
        for (i=0; i<k; i++){
                for(j=i+1; j<k&&j<i+7; j++){
                        if ((point[temp[i]].y - point[temp[j]].y)*(point[temp[i]].y - point[temp[j]].y) <End_dis)
                                End_dis = mindistance(End_dis,distance(temp[i],temp[j]));
                }
        }
        return End_dis;        
}

int main(){
        int n,i;
        scanf("%d",&n);
        for(i=0;i<n;i++){
                scanf ("%d %d",&point[i].x,&point[i].y);
        }
        qsort(point,n,sizeof(point[0]),cmp);
        printf("%d\n",Closest_Pair(0,n-1));
        return 0;
}

这个代码第一个测试用例就过不去，我想请问一下问题出在哪里
同时，假如我把数组开到10^6，不管我输入什么，都会出现下图问题

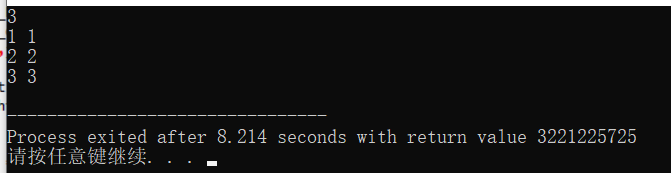
想请教一下大家问题出在哪里，谢谢！

最佳答案

月排行榜 / 总排行榜

jhq999

2021-10-31 01:11:04

静态数组定义的太大了。

int Closest_Pair(int left,int right){
        int End_dis = INF;
        int i=0,j=0,k=0;
        
        if (left == right) return End_dis;//假如区间里面只有一个点，那么返回无穷大 
        if (right - left == 1) return distance(left,right);//假如区间里面只有两个点，那么直接返回这两点之间距离的平方
         
        
        int mid = (left + right)/2;//计算中线，判断是否是大于等于三个点的情况
        
        int distanceleft  = Closest_Pair(left,mid);//左边递归 
        int distanceright = Closest_Pair(mid+1,right);//右边递归
        
        End_dis = mindistance(distanceleft,distanceright) ;//比较左右两边距离的平方，找出最小值，即为d 
        //////////
        int *temp = new int[N]; //储存宽度为d的点
        //////////
        for (i = left; i < right; i++){//找出符合要求的距离mid横坐标的平方小于d的点 
                if ( (point[left].x - point[right].x)*(point[left].x - point[right].x) <= End_dis ){
                        temp[k++] = i;//temp用来暂时存储符合要求的点的序号 
                }
        } 
        for (i=0; i<k; i++){
                for(j=i+1; j<k&&j<i+7; j++){
                        if ((point[temp[i]].y - point[temp[j]].y)*(point[temp[i]].y - point[temp[j]].y) <End_dis)
                                End_dis = mindistance(End_dis,distance(temp[i],temp[j]));
                }
        }
                delete[] temp;////////////
        return End_dis;        
}

跳转到最佳答案楼层

jhq999

静态数组定义的太大了。

int Closest_Pair(int left,int right){
        int End_dis = INF;
        int i=0,j=0,k=0;
        
        if (left == right) return End_dis;//假如区间里面只有一个点，那么返回无穷大 
        if (right - left == 1) return distance(left,right);//假如区间里面只有两个点，那么直接返回这两点之间距离的平方
         
        
        int mid = (left + right)/2;//计算中线，判断是否是大于等于三个点的情况
        
        int distanceleft  = Closest_Pair(left,mid);//左边递归 
        int distanceright = Closest_Pair(mid+1,right);//右边递归
        
        End_dis = mindistance(distanceleft,distanceright) ;//比较左右两边距离的平方，找出最小值，即为d 
        //////////
        int *temp = new int[N]; //储存宽度为d的点
        //////////
        for (i = left; i < right; i++){//找出符合要求的距离mid横坐标的平方小于d的点 
                if ( (point[left].x - point[right].x)*(point[left].x - point[right].x) <= End_dis ){
                        temp[k++] = i;//temp用来暂时存储符合要求的点的序号 
                }
        } 
        for (i=0; i<k; i++){
                for(j=i+1; j<k&&j<i+7; j++){
                        if ((point[temp[i]].y - point[temp[j]].y)*(point[temp[i]].y - point[temp[j]].y) <End_dis)
                                End_dis = mindistance(End_dis,distance(temp[i],temp[j]));
                }
        }
                delete[] temp;////////////
        return End_dis;        
}

傻眼貓咪

n 不超过 1000000
x、y不超过 10000
以你的代码时间复杂度，不超时（TLE）吗？

William_Prince

jhq999 发表于 2021-10-31 01:11
静态数组定义的太大了。

谢谢！这段改完之后还是有一个超时，然后我把数组开到全局变量里头就过了。