|
|
60鱼币
题目2:中国邮递员问题的研究与实现
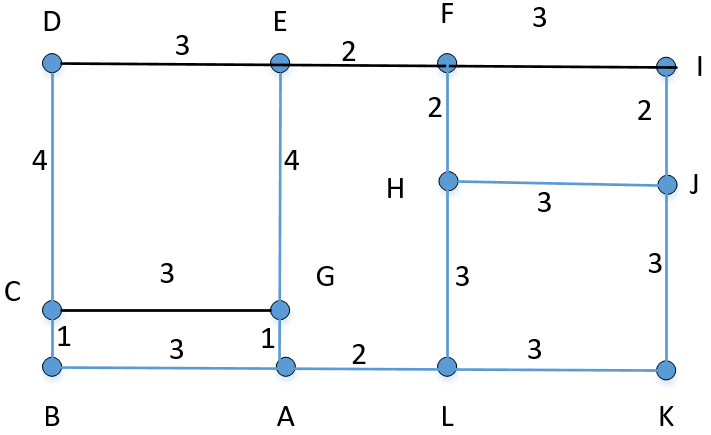
邮递员投递区如下图所示,街道边的数字为邮递员行走所用的时间代价,★表示邮局,邮递员从邮局出发走遍每条街道,最后返回邮局,请设计一条代价最小的行走线路,该问题为“邮递员”问题。
图1:街区无向图
问题描述如下:邮递员从邮局(A)出发走遍每条街道,最后返回邮局,邮递员应按怎样的顺序投递,才能使经过的路径长度最小。本题的原型是著名的“一笔画”问题。根据图论的定理可知,任何一个图若要能一笔画成,则必须同时满足以下两个条件,其一:该图是连通的;其二:图中度数为奇数的点(又称为奇度点)的个数为不多于两个。
在图中,共有A、C、E、F、G、H、J、L等8个奇度点,因此该图不一笔画成,即邮递员从邮局出发,要想走遍所有街道,某些街道必定会重复经过。因此,此问题的关键在于如何向图中“添加”若干条代价最小的边,使得此图最终满足一笔画的条件。
要解决此问题,提示:
其一:“添加”哪些边?
显然,“添加”的边所依附的顶点必须均是奇度点。图中有8个奇度点,可以组合成4条边,使得奇度点的个数为0个。
其二:如何选择代价最小的边?
因为图中8个奇度顶点组合成4条边的情形有很多种,所以要分别求出每种组合形成的边的代价,然后从中选出代价最小的边。
另外,在此问题中,边的“添加”的应该理解为从一个奇度点到另一个奇度点之间的路径。
“邮递员”问题要求实现以下功能:
(1)建立街区无向网的邻接矩阵;
(2)求各顶点的度数;
(3)求出所有奇度点;
(4)求出每一个奇度点到其它奇度点的最短路径;
(5)找出距离最短的添加方案;
(6)根据最佳方案添加边,使之满足一笔画的条件;
(7)对图进行一笔画,并输出。 |
-
图1街区无向图
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)