|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
MaxMin算法(极大极小值算法)
该算法是一种找出失败的最大可能性中的最小值的算法(即最小化对手的最大得益)。通常以递归形式来实现。
Minimax算法常用于棋类等由两方较量的游戏和程序。该算法是一个零总和算法,即一方要在可选的选项中选择将其优势最大化的选择,另一方则选择令对手优势最小化的一个,其输赢的总和为0。
其实一般不太建议用这种算法,不过由于这个是AlphaBeta剪枝算法的前置,所有这里还是介绍一下。
介绍这个算法前,简单的介绍一下博弈树。如下图井子琪游戏为例,这只是一个简略的博弈树,整个博弈树有多少个节点的呢?答案是9!,共计362880个节点。而该算法则会尽心尽力的去搜遍这362880个节点。所以这是一个不“太聪明”的算法,也型号,这个是可以改进的,这里暂且不提。
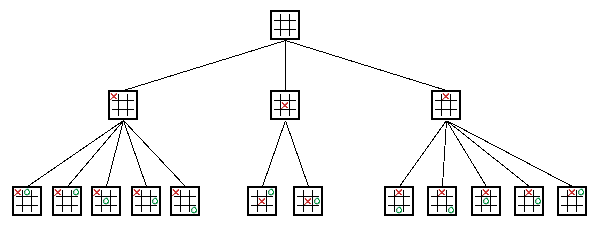
MINMAX的基本思想,我们程序在搜索完成井子琪游戏的博弈树之后,可以知道所有的游戏的结局,知道哪个分枝会输,知道哪个分枝会赢,或者平局。既然知道结局,那么把结果传播回去就可以,假定电脑赢游戏,对游戏给定 1 分的评价,电脑输游戏,给对游戏给定 -1 分的评价,如果是平局,对游戏给定 0 分的评价。并且假定对手是非常聪明的,他落子的时候,总会选择最优的局面,对电脑而言就是最差的局面。
python伪代码实现
- def MiniMaxAlgorithm(int: depth, flag):
- # depth:: 是深度的意思,对于一些游戏树是深不可达,所以一般扩展到某一个游戏状态就停止了
- # 定义递归出口,或者是游戏结束状态,返回当前游戏状态的评分
- if (depth==0 and GameOver):
- # 评分函数,赢了,输了,平局,会在自己定义响应的规则评分
- return EvaluationFunction(Gs)
- MaxValue = float('-inf')
- MinValue = float('inf')
- # 测试所有合法的着点
- for Move in GeneratorMoves:
- # 执行着点
- MakeNextMove()
- # 交换身份,继续,
- score = MiniMaxAlgorithm(depth-1, falg)
- # 撤销着点
- UnMakeNextMove()
- # 如果当前是电脑走步落子
- if flag is Max:
- MaxValue = max(score, MaxValue)
- else:
- MinValue = min(socre, MinValue)
- if flag is Max:
- return Maxvalue
- else:
- return MinValue
|
评分
-
查看全部评分
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)