|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
原理:
备注:
算法:
- #include <stdio.h>
- #include <stdlib.h>
- #define MAX 65535
- int KA[4][4] = {{0, 2, 6, 4}, {MAX, 0, 3, MAX}, {7, MAX, 0, 1}, {5, MAX, 12, 0}};
- int main()
- {
- //佛洛依德算法需要经过3个for循环第一个
- for(int k = 0; k < 4; k++) //这个循环是他经过的那个节点
- {
- for(int i = 0; i < 4; i++) //从经过的那个节点开始横向比较
- {
- for(int j = 0; j < 4; j++) //从经过的那个节点开始竖向比较
- {
- if((i != j) && (i != k) && (j != k) && KA[i][j] > KA[i][k] + KA[k][j]) //比较的前提是i不等于j、i不等于k、j不等于k,总体含义是自己不等于自己,这可以减少运算,然后才是判断竖排的数与横向的数相加是否小于没格循环的数如果小于那就执行,替换掉i-j单元中的数据
- {
- KA[i][j] = KA[i][k] + KA[k][j]; //数据替换
- }
- }
- }
- }
- for(int i = 0; i < 4; i++)
- {
- for(int j = 0; j < 4; j++)
- {
- printf("%d ", KA[i][j]);
- }
- putchar('\n');
- }
- return 0;
- }
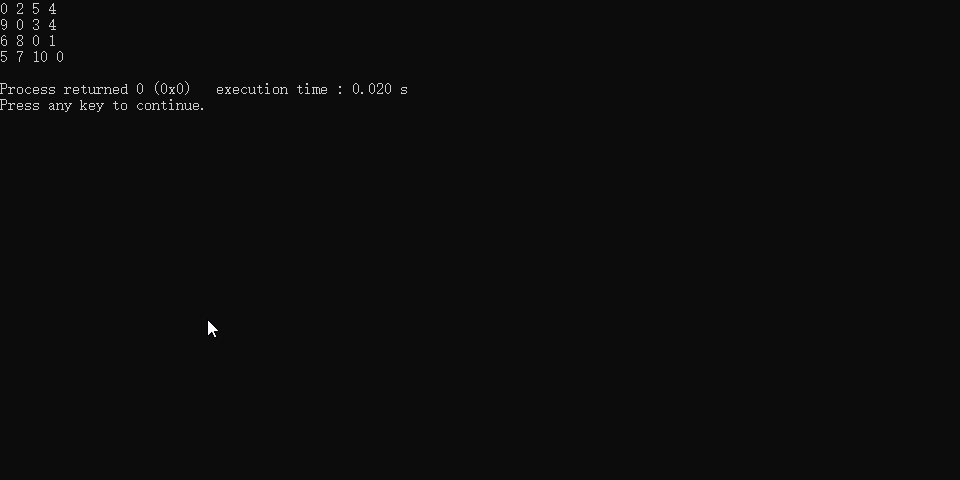
输出结果:
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)