题目65：找出e的连分数中第100个收敛项的分子各位之和。

欧拉计划

Convergents of e

The square root of 2 can be written as an infinite continued fraction.



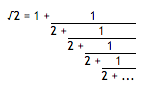
The infinite continued fraction can be written, 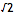= [1;(2)], (2) indicates that 2 repeats ad infinitum. In a similar way, 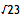= [4;(1,3,1,8)].

It turns out that the sequence of partial values of continued fractions for square roots provide the best rational approximations. Let us consider the convergents for .



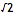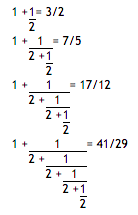
Hence the sequence of the first ten convergents for 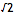are:

1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, ...
What is most surprising is that the important mathematical constant,
e = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...].

The first ten terms in the sequence of convergents for e are:

2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, ...
The sum of digits in the numerator of the convergent is 1+4+5+7=17.

Find the sum of digits in the numerator of the 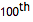convergent of the continued fraction for e.

题目：

2的平方根可以写作无限连分数：



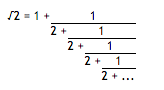
这个无限连分数可以写作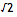， = [1;(2)], (2) 表示2无限循环出现。类似的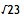， = [4;(1,3,1,8)]。

事实证明平方根的连分数序列提供了最好的有理数近似值。让我们考虑 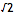的收敛项：



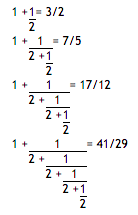
因此 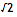的收敛项中的前十项是：

1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, ...

更令人惊奇的是一个重要的数学常数：

e = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...].

e 的收敛项序列中的前十项是：

2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, ...

其中第十项的分子各位数之和是 1+4+5+7=17。

找出 e 的收敛项序列中第 100 项的分子上各位之和。

jerryxjr1220

1. 272
   
2. [Finished in 0.1s]

复制代码

本来写了递归的算法，结果run了半天出不来，果然递归的效率太低，用列表就快多了

1. k = []
   
2. for i in range(34):
   
3.         k.append (1)
   
4.         k.append (2*i+2)
   
5.         k.append (1)
   
6. 
   
7. En = [2,3]
   
8. for j in range(2,101):
   
9.         En.append (En[j-1] * k[j-1] + En[j-2])
   
10. 
    
11. E100 = str(En[99])
    
12. total = 0
    
13. for each in E100:
    
14.         total += int(each)
    
15. print (total)

复制代码

99592938

1. def con_e(num):#将连分数e的前num项组成list
   
2.     e=[2]
   
3.     for i in range(1,num):
   
4.         if i%3==2:
   
5.             e.append(2*i//3+1)
   
6.         else:
   
7.             e.append(1)
   
8.     return e
   
9. 
   
10. def deno(num):#将c+1/(b/a)转为b/a的格式,迭代c，最后一项不倒置，所以a即num项的分子
    
11.     e=con_e(num)
    
12.     a=e.pop()
    
13.     b=1
    
14.     while len(e):
    
15.         c=e.pop()
    
16.         temp=a*c+b
    
17.         b=a
    
18.         a=temp
    
19.     return a
    
20. 
    
21. num=100
    
22. print(sum(int(i) for i in str(deno(num))))

复制代码

272
>>>

najin

用matlab算这个题目就是艹蛋，放弃

fc1735

1. from fractions import Fraction
   
2. 
   
3. def fun(n):
   
4.   if n == 0:
   
5.     return 2
   
6.   elif n % 3 == 2:
   
7.     return (n + 1) * 2 // 3
   
8.   else:
   
9.     return 1
   
10. 
    
11. ans = Fraction(0)
    
12. for i in map(lambda x: fun(x), reversed(range(100))):
    
13.   ans += i
    
14.   ans = 1 / ans
    
15. 
    
16. print(sum(map(lambda x: int(x), str(ans.denominator))))
    

复制代码

https://github.com/devinizz/project_euler/blob/master/page02/65.py

j.p.-hwang

1. n=99;
   
2. k=ones(1,n);
   
3. k(2:3:end)=2*(1:round(n/3));
   
4. k=flip(k);
   
5. fenzi=sym('1');
   
6. fenmu=sym(k(1));
   
7. for i=2:n
   
8.     temp=sym(fenmu);
   
9.     fenmu=sym(fenzi+k(i)*temp);
   
10.     fenzi=temp;
    
11. end
    
12. total=[fenzi+2*fenmu fenmu];
    
13. t1=char(total(1));
    
14. wei=length(t1);
    
15. s=0;
    
16. for j=1:wei
    
17.     s=s+str2num(t1(j));
    
18. end

复制代码

永恒的蓝色梦想

j.p.-hwang 发表于 2020-6-28 15:18
n=99;
k=ones(1,n);
k(2:3:end)=2*(1:round(n/3));

这……是什么语言

debuggerzh

272

Process returned 0 (0x0)   execution time : 0.032 s
Press any key to continue.
使用栈储存数据，递推计算，大数

1. #include<iostream>
   
2. #include<vector>
   
3. #include<stack>
   
4. using namespace std;
   
5. 
   
6. typedef struct BigInt{
   
7.   vector<int> v;
   
8. 
   
9.   BigInt(vector<int> v):v(v){}
   
10. }BI;
    
11. 
    
12. BI operator + (const BI & a,const BI & x){
    
13.   vector<int> t1 = a.v;
    
14.   vector<int> t2 = x.v;
    
15.   if (a.v.size() < x.v.size())  swap(t1,t2);
    
16. 
    
17.   for (int i = 0;i < max(t1.size(),t2.size() );i++){
    
18.       if (i < t2.size())  t1[i] += t2[i];
    
19.       if (i > 0 && t1[i-1] > 9)  {t1[i]++;  t1[i-1] -= 10;}
    
20.   }
    
21. 
    
22.   if (t1[t2.size()-1] > 9)
    
23.     if (t1.size() == t2.size() )  {t1.push_back(1);  t1[t1.size()-2] -= 10;}
    
24. 
    
25.     else {
    
26.       t1[t2.size()]++;
    
27.       for (int i = t2.size();i < t1.size()-1;i++){
    
28.         if (t1[i] > 9) {t1[i] -= 10;  t1[i+1]++;}
    
29.         else break;
    
30.       }
    
31.       t1[t2.size()-1] -= 10;
    
32.     }
    
33.   return BI(t1);
    
34. }
    
35. 
    
36. BI operator * (const int c,const BI & x){
    
37.   BI res = x;
    
38. 
    
39.   for (int i = 0;i < res.v.size();i++)
    
40.     res.v[i] *= c;
    
41. 
    
42.   for (int i = 0;i < res.v.size()-1;i++)
    
43.     if (res.v[i] > 9) {
    
44.       res.v[i+1] += res.v[i] / 10;
    
45.       res.v[i] %= 10;
    
46.   }
    
47.   int sz = res.v.size();
    
48.   if (res.v[sz-1] > 9)  {res.v.push_back(res.v[sz-1] / 10); res.v[sz-1] %= 10;}
    
49. 
    
50.   return res;
    
51. }
    
52. 
    
53. void print_ans(const BI & x){
    
54.   int ans = 0;
    
55. 
    
56.   for (int i = 0;i < x.v.size();i++)
    
57.     ans += x.v[i];
    
58. 
    
59.   cout << ans <<endl;
    
60. }
    
61. 
    
62. int main()
    
63. {
    
64.   vector<int> a(1,1),b(1,1);
    
65.   BI n(a),d(b);
    
66.   stack<int> s;
    
67. 
    
68.   for (int i = 1;i < 99;i++){
    
69.     int k = i/3 + 1;
    
70. 
    
71.     if (i % 3 == 2) s.push(2*k);
    
72.     else  s.push(1);
    
73.   }
    
74.   while(s.size() ){//先算e-2，再补回去
    
75.     //cout << s.top() << endl;
    
76.     BI t = d;
    
77.     d = n + s.top() * d;
    
78.     n = t;
    
79. 
    
80.     s.pop();
    
81.   }
    
82.   n = n + 2*d;
    
83. 
    
84.   print_ans(n);
    
85.   return 0;
    
86. }
    

复制代码

guosl

1. /*
   
2. 答案：272
   
3. */
   
4. #include <iostream>
   
5. #include <string>
   
6. #include <gmpxx.h>
   
7. using namespace std;
   
8. 
   
9. int main(void)
   
10. {
    
11.   mpz_class p1 = 2, p2 = 3, p3, q1 = 1, q2 = 1, q3;
    
12.   for (int i = 3; i <= 100; ++i)
    
13.   {
    
14.     if (i % 3 == 0)
    
15.     {
    
16.       p3 = p2 * 2 * (i / 3) + p1;
    
17.       q3 = q2 * 2 * (i / 3) + q1;
    
18.     }
    
19.     else
    
20.     {
    
21.       p3 = p2 + p1;
    
22.       q3 = q2 + q1;
    
23.     }
    
24.     p1 = p2;
    
25.     q1 = q2;
    
26.     p2 = p3;
    
27.     q2 = q3;
    
28.   }
    
29.   string str = p2.get_str(10);
    
30.   int nSum = 0;
    
31.   for(int i = 0; i < int(str.length()); ++i)
    
32.     nSum += int(str[i] - 48);
    
33.   cout << nSum << endl;
    
34.   return 0;
    
35. }
    

复制代码

永恒的蓝色梦想

1. def generator():
   
2.     yield 2
   
3.     k = 2
   
4. 
   
5.     while True:
   
6.         yield 1
   
7.         yield k
   
8.         yield 1
   
9.         k += 2
   
10. 
    
11. it = [i for i, _ in zip(generator(), range(100))]
    
12. it.reverse()
    
13. it = iter(it)
    
14. 
    
15. nume = next(it)
    
16. deno = 1
    
17. 
    
18. for i in it:
    
19.     nume, deno = i * nume + deno, nume
    
20. 
    
21. print(sum(int(i) for i in str(nume)))

复制代码

guosl

本题可以应用连分数的递推公式和大数库mpir（或gmp）来解。

1. /*
   
2. 答案：272
   
3. */
   
4. #include <iostream>
   
5. #include <string>
   
6. #include <mpirxx.h>
   
7. using namespace std;
   
8. 
   
9. int main(void)
   
10. {
    
11.   mpz_class p1=2, p2=3, p3;
    
12.   mpz_class q1=1, q2=1, q3;
    
13.   for (int i = 3; i <= 100; ++i)
    
14.   {
    
15.     int a = 1;
    
16.     if (i % 3 == 0)
    
17.       a = (i / 3) * 2;
    
18.     p3 = a*p2 + p1;
    
19.     q3 = a*q2 + q1;
    
20.     p1 = p2;
    
21.     p2 = p3;
    
22.     q1 = q2;
    
23.     q2 = q3;
    
24.   }
    
25.   string str = p3.get_str();
    
26.   int nSum = 0;
    
27.   for (int i = 0; i < (int)str.length(); ++i)
    
28.     nSum += int(str[i] - '0');
    
29.   cout << nSum << endl;
    
30.   return 0;
    
31. }

复制代码

B1tetheDust

1. import time as t
   
2. 
   
3. start = t.perf_counter()
   
4. decimal_list = []
   
5. for n in range(2, 101):
   
6.     if not n % 3:
   
7.         decimal_list.append(n // 3 * 2)
   
8.     else:
   
9.         decimal_list.append(1)
   
10. 
    
11. numerator = 1
    
12. denominator = decimal_list[-1]
    
13. for n in range(98, 0, -1):
    
14.     numerator, denominator = denominator, numerator + denominator * decimal_list[n - 1]
    
15. numerator += denominator * 2
    
16. print(sum([int(i) for i in str(numerator)]))
    
17. print("It costs %f s" % (t.perf_counter() - start))
    

复制代码

272
It costs 0.000073 s

TLM

永恒的蓝色梦想 发表于 2020-6-28 16:17
这……是什么语言

matlab，虽然已经三年了