|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
Totient permutation
Euler's Totient function, φ(n) [sometimes called the phi function], is used to determine the number of positive numbers less than or equal to n which are relatively prime to n. For example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, φ(9)=6.
The number 1 is considered to be relatively prime to every positive number, so φ(1)=1.
Interestingly, φ(87109)=79180, and it can be seen that 87109 is a permutation of 79180.
Find the value of n, 1 < n <
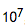 , for which φ(n) is a permutation of n and the ratio n/φ(n) produces a minimum.
, for which φ(n) is a permutation of n and the ratio n/φ(n) produces a minimum.
题目:
欧拉函数 φ(n)(有时也叫做phi函数)可以用来计算小于等于 n 的数字中与 n 互质的数字的个数。例如,因为 1,2,4,5,7,8 全部小于 9 并且与 9 互质,所以φ(9)=6。
数字1被认为与每个正整数互质,所以 φ(1)=1。
有趣的是,φ(87109)=79180,可以看出 87109 是 79180 的一个排列。
对于 1 < n <
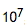 ,并且 φ(n) 是 n 的一个排列的那些 n 中,使得 n/φ(n) 取到最小的 n 是多少?
,并且 φ(n) 是 n 的一个排列的那些 n 中,使得 n/φ(n) 取到最小的 n 是多少?
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)