|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.linspace(0,80,50)
y1 = (2*x/(1+x))**0.5-1+1/(x**0.5)*(1-(2/(1+x))**0.5)
y2 = 2**0.5 -1+(1/x**0.5)*(2**0.5-1)
plt.title('Transfer')
plt.xlabel('R')
plt.ylabel('Required V[ /Vi]')
plt.plot(x,y1)
plt.plot(x,y2)
plt.show()
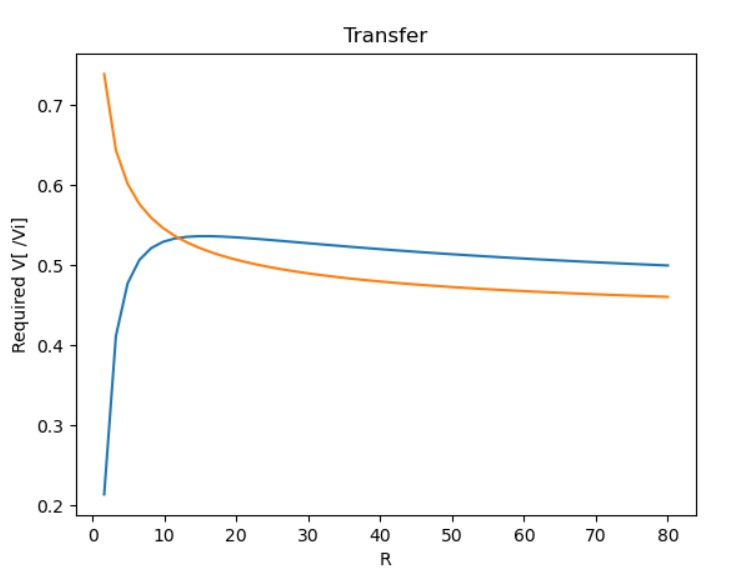
交点的横坐标怎么求T T以及交点的纵坐标,还有交点的话可以在图中标记出来吗?
初学Python,拿来做一个作业,但无奈知识太欠缺,在此先谢过!
本帖最后由 java2python 于 2020-6-1 02:33 编辑
其实这个问题个人是随意发表意见的,应该也算一种方法
首先解方程肯定是不予考虑的,数学太难了,无非是利用计算机的超强计算力,进行大量循环查找。
所谓交点,会产生位置关系变动(也不能绝对,还有相切的),原先黄线在上,焦点过后,黄线在下,当然一般函数都是连续的。。。
找到了这个区间,比如[10,20]之间发生,在采用两分法,到底是[10,15],还是[15,20]区间,
如此直到区间足够小,双方差距足够小,认为这点就是交点。如果其实区间是[10,20]
采用10次可以精确到0.01
采用20次可以精确到0.00001
采用20次可以精确到0.00000001
...
再下去就小于宇宙中的任何尺寸了,不过数学上的精确是永远无法达到的的,除非这个交点是一个有限小数,连有理数(无限但循环)也搞不定
图中标记就简单了,因为计算机显示器上的图是按像素来的,都是千分之一精度的
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)