|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
知识点回顾:
1. 绘制折线的几个函数
Polyline —— 绘制一条折线
PolylineTo —— 绘制一条折线(修改当前位置为折线结束位置)
PolyPolyline —— 绘制多条折线
2. 绘制正弦函数:y = sinx
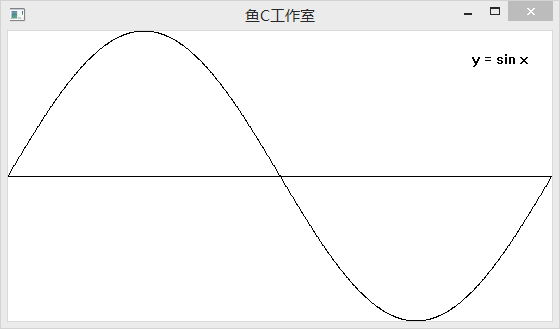
利用折线绘制“曲线”是编程中通用的做法,当折线的每两个点之间的距离非常小时,看上去就是一条曲线。
下边是绘制 y = sinx 的主要代码,重点部分做了注释:
- #include <math.h>
- // 因为是使用折线绘画,所以当折线的顶点数量非常多的时候,我们就可以看到一条近似完美的曲线了!
- #define NUM 1000 // 将 x 轴分成 1000 等份
- #define TWOPI (2 * 3.14159) // 一个周期等于 2π
- ……
- LRESULT CALLBACK WndProc(HWND hwnd, UINT message, WPARAM wParam, LPARAM lParam)
- {
- HDC hdc;
- PAINTSTRUCT ps;
- static int cxClient, cyClient;
- POINT apt[NUM]; // 一千个点构成
- int i;
- switch (message)
- {
- /* 首先,我们需要让窗口在改变大小的时候,sin 函数的图形会跟着实时改变,所以我们这里需要响应 WM_SIZE 消息,
- lParam 的低 16 位是客户区的宽,高 16 位是客户区的高。
- */
- case WM_SIZE:
- cxClient = LOWORD(lParam);
- cyClient = HIWORD(lParam);
- return 0;
- case WM_PAINT:
- hdc = BeginPaint(hwnd, &ps);
- // 先画一条 x 轴在客户区的 1/2 的位置
- MoveToEx(hdc, 0, cyClient / 2, NULL);
- LineTo(hdc, cxClient, cyClient / 2);
- // 接着我们用一个循环,分别求出每个 x 对应的 y 值,然后把它画出来即可。
- for (i = 0; i < NUM; i++)
- {
- // 将 x 分为 1000 等份,然后将每一份的 x 坐标计算出来。
- apt[i].x = i * cxClient / NUM;
- /* 直接调用 sin 函数计算 y 值:api[i].y = (int)(sin(x))
- 这里我们要显示一个周期(2π):api[i].y = (int)(sin(TWOPI * i / NUM))
- 接下来是难点了:
- 要把求得的 y 值显示在整个客户区内,正弦函数 y 值的取值范围是 -1 ~ 1,
- 而我们的客户区是木有负数的范围,而且数学函数原点的位置跟客户区原点的位置不同,
- 导致直接显示到客户区上的图像会倒过来。
- 所以我们应该做一些转化:1 - sin(TWOPI * i / NUM)
- 使得函数图像倒过来,并且 y 值的取值范围变成了 0 ~ 2,
- 所以这里我们再乘上 cyClient / 2 即可完美显示!
- */
- apt[i].y = (int)(cyClient / 2 * (1 - sin(TWOPI * i / NUM)));
- }
- PolylineTo(hdc, apt, NUM);
- EndPaint(hwnd, &ps);
- return 0;
- case WM_DESTROY:
- PostQuitMessage(0);
- return 0;
- }
- return DefWindowProc(hwnd, message, wParam, lParam);
- }
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)