一个Sqrt函数引发的血案

太子

好吧，我承认我标题党了，不过既然你来了，就认真看下去吧，保证你有收获。网上看到的
我们平时经常会有一些数据运算的操作，需要调用sqrt，exp，abs等函数，那么时候你有没有想过：这个些函数系统是如何实现的？就拿最常用的sqrt函数来说吧，系统怎么来实现这个经常调用的函数呢？
虽然有可能你平时没有想过这个问题，不过正所谓是“临阵磨枪，不快也光”，你“眉头一皱，计上心来”，这个不是太简单了嘛，用二分的方法，在一个区间中，每次拿中间数的平方来试验，如果大了，就再试左区间的中间数；如果小了，就再拿右区间的中间数来试。比如求sqrt(16)的结果，你先试（0+16）/2=8，8*8=64，64比16大，然后就向左移，试（0+8）/2=4，4*4=16刚好，你得到了正确的结果sqrt(16)=4。然后你三下五除二就把程序写出来了：

float SqrtByBisection(float n) //用二分法
{
        if(n<0) //小于0的按照你需要的处理
                return n;
        float mid,last;
        float low,up;
        low=0,up=n;
        mid=(low+up)/2;
        do
        {
                if(mid*mid>n)
                        up=mid;
                else
                        low=mid;
                last=mid;
                mid=(up+low)/2;
        }while(abs(mid-last) > eps);//精度控制
        return mid;
}

然后看看和系统函数性能和精度的差别（其中时间单位不是秒也不是毫秒，而是CPU Tick，不管单位是什么，统一了就有可比性）

                               
登录/注册后可看大图

从图中可以看出，二分法和系统的方法结果上完全相同，但是性能上整整差了几百倍。为什么会有这么大的区别呢？难道系统有什么更好的办法？难道。。。。哦，对了，回忆下我们曾经的高数课，曾经老师教过我们“牛顿迭代法快速寻找平方根”，或者这种方法可以帮助我们，具体步骤如下：

求出根号a的近似值：首先随便猜一个近似值x，然后不断令x等于x和a/x的平均数，迭代个六七次后x的值就已经相当精确了。

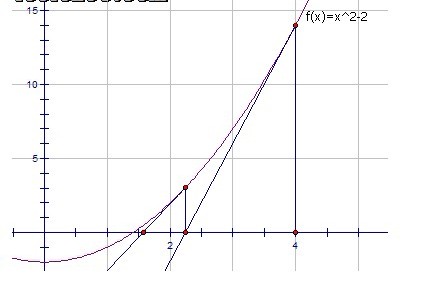例如，我想求根号2等于多少。假如我猜测的结果为4，虽然错的离谱，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了：(       4  + 2/4        ) / 2 = 2.25(     2.25 + 2/2.25     ) / 2 = 1.56944..( 1.56944..+ 2/1.56944..) / 2 = 1.42189..( 1.42189..+ 2/1.42189..) / 2 = 1.41423..…. file:///C:\Users\CaiXiaoyu\AppData\Roaming\Tencent\Users\470572797\QQ\WinTemp\RichOle\@2HIE]BM)GLBX~V}EM%N`VG.jpg 这种算法的原理很简单，我们仅仅是不断用(x,f(x))的切线来逼近方程x^2-a=0的根。根号a实际上就是x^2-a=0的一个正实根，这个函数的导数是2x。也就是说，函数上任一点(x,f(x))处的切线斜率是2x。那么，x-f(x)/(2x)就是一个比x更接近的近似值。代入 f(x)=x^2-a得到x-(x^2-a)/(2x)，也就是(x+a/x)/2。相关的代码如下：

float SqrtByNewton(float x)
{
        float val = x;//最终
        float last;//保存上一个计算的值
        do
        {
                last = val;
                val =(val + x/val) / 2;
        }while(abs(val-last) > eps);
        return val;
}

然后我们再来看下性能测试：

                               
登录/注册后可看大图

哇塞，性能提高了很多，可是和系统函数相比，还是有这么大差距，这是为什么呀？想啊想啊，想了很久仍然百思不得其解。突然有一天，我在网上看到一个神奇的方法，于是就有了今天的这篇文章，废话不多说，看代码先：

float InvSqrt(float x)
{
        float xhalf = 0.5f*x;
        int i = *(int*)&x; // get bits for floating VALUE
        i = 0x5f375a86- (i>>1); // gives initial guess y0
        x = *(float*)&i; // convert bits BACK to float
        x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
        x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
        x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy

        return 1/x;
}

然后我们最后一次来看下性能测试：

                               
登录/注册后可看大图

这次真的是质变了，结果竟然比系统的还要好。。。哥真的是震惊了！！！哥吐血了！！！一个函数引发了血案！！！血案，血案。。。

                               
登录/注册后可看大图

该贴已经同步到 太子的微博

ever.g

不错 看来这个方法很神奇，不过指针
我就知道我暂时看不懂就是了~~

surongre

make先，以后研究研究

醉笑遥

好强的贴啊

Love 梦想

问下 你是怎么测出时间的？

ylo523

真是厉害，顶一个

feitianqu

picture no display

飞鸽

赞一个:lol

我是师兄

雷神之锤的那个 神秘的0x5f375a86

那是一个传奇

☆小韦QQ

牛人啊！我只是路过打酱油的。

bafengao

感恩无私的分享与奉献 :)

mcx88

现在虽然看不懂，不过也知道，这太强了。

未闻丶花名

路过看一看= =！

a471893438

靠，后悔没高数没学了，这么牛叉

jiangyuming0434

楼主很聪明也很诚实。