006-栈

moc

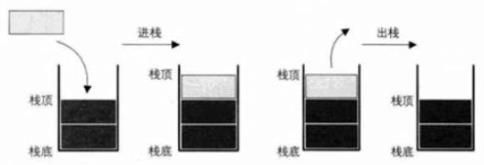
1、栈的基本概念
栈是一种   特殊的线性表。
它的特殊之处在于限制了这个线性表的插入和删除位置，它始终只在栈顶进行，这也就使得：栈底是固定的，最先进栈的只能在栈底。
栈是仅能在一端操作的线性表：
        栈顶（Top）：允许操作的一端；
        栈底（Bottom）：不允许操作的一端。
栈的插入操作，叫做进栈，压栈，入栈。
栈的删除操作，叫做出栈，弹栈。

Stack的常用操作：
        创建栈；
        销毁栈；
        清空栈；
        进栈；
        出栈；
        获取栈顶元素；
        获取栈的大小。
2、栈的顺序存储及实现
栈是一种特殊的线性表，所以实现顺序存储的栈  可以在顺序存储的线性表的基础上来实现。
当用线性表的顺序存储来模拟栈时，如果把线性表的尾部作为栈顶，不会涉及到栈元素的大小大量移动，效率更高。

// 创建栈  相当于  创建线性表
SeqStack* SeqStack_Create(int capacity)
{
        return SeqList_Create(capacity);
}

// 销毁栈  相当于  销毁线性表
void SeqStack_Destroy(SeqStack* stack)
{
        SeqList_Destroy(stack);
}

// 清空栈  相当于  清空线性表
void SeqStack_Clear(SeqStack* stack)
{
        SeqList_Clear(stack);
}

// 向栈中压入元素 相当于 向链表的尾部插入元素
int SeqStack_Push(SeqStack* stack, void* item)
{
        return SeqList_Insert(stack, item, SeqList_Length(stack));
}

// 从栈中弹出元素 相当于 从链表的尾部取出元素
void* SeqStack_Pop(SeqStack* stack)
{
        return SeqList_Delete(stack, SeqList_Length(stack) - 1);
}

// 获取栈顶元素 相当于 获取链表的尾部元素
void* SeqStack_Top(SeqStack* stack)
{
        return SeqList_Get(stack, SeqList_Length(stack) - 1);
}

// 获取栈的大小 相当于 获取链表的实际长度
int SeqStack_Size(SeqStack* stack)
{
        return SeqList_Length(stack);
}

// 获取栈的容量 相当于 获取链表的实际容量
int SeqStack_Capacity(SeqStack* stack)
{
        return SeqList_Capacity(stack);
}

3、栈的链式存储及实现
同样可以用线性表的链式存储来   模拟 栈的链式存储结构。
需要注意：
        ① 在入栈时，需要将栈的业务结点（void*）  转化为  线性表的业务结点（TLinkStackNode*）；
        ② 栈结点是malloc而来的   于是要进行栈结点的生命周期管理

typedef struct  _tag_LinkStackNode // 链表的业务结点
{
        LinkListNode node;   
        void* item;   // 栈的业务结点
}TLinkStackNode;

// 创建栈  相当于  创建线性表
LinkStack* LinkStack_Create()
{
        return LinkList_Create();
}

// 销毁栈  相当于  销毁线性表
void LinkStack_Destroy(LinkStack* stack)
{
        LinkStack_Clear(stack);
        LinkList_Destroy(stack);
}

// 清空栈  相当于  清空线性表
// 清空栈的时候 涉及到 栈元素生命周期的管理
// 所有入栈的元素都是 malloc过的，清空时需要弹出栈中所有元素
void LinkStack_Clear(LinkStack* stack)
{
        if (stack == NULL)
        {
                return;
        }
        while (LinkStack_Size(stack) > 0)
        {
                LinkStack_Pop(stack);  // 在此函数中释放内存
        }
}

// 向栈中压入元素 相当于 向链表的头部插入元素
// void* item 栈的业务结点   --->  链表的业务结点
int LinkStack_Push(LinkStack* stack, void* item)
{
        int ret = 0;
        TLinkStackNode *tmp = NULL;
        tmp = (TLinkStackNode*)malloc(sizeof(TLinkStackNode));
        if (tmp == NULL)
        {
                return -1;
        }
        memset(tmp, 0, sizeof(TLinkStackNode));
        tmp->item = item;

        ret = LinkList_Insert(stack, (LinkListNode*)tmp, 0);
        if (ret != 0)
        {
                printf("Fun LinkList_Insert Error: %d\n", ret);
                if (tmp != NULL)
                {
                        free(tmp);
                }
        }
        return ret;
}

// 从栈中弹出元素 相当于 从链表的头部取出元素
void* LinkStack_Pop(LinkStack* stack)
{
        void* item = NULL;  // 栈的业务结点
        TLinkStackNode *tmp = NULL;
        tmp = (TLinkStackNode*)LinkList_Delete(stack, 0);
        if (tmp == NULL)
        {
                return NULL;
        }
        item = tmp->item;
        // 在入栈时分配了内存，所以在出栈时需要释放内存
        free(tmp);
        return item;
}


// 获取栈顶元素 相当于 获取链表的头部元素
void* LinkStack_Top(LinkStack* stack)
{
        TLinkStackNode *tmp = NULL;
        tmp = (TLinkStackNode*)LinkList_Get(stack, 0);
        if (tmp == NULL)
        {
                return NULL;
        }
        return tmp->item;
}

// 获取栈的大小 相当于 获取链表的实际长度
int LinkStack_Size(LinkStack* stack)
{
        return LinkList_Length(stack);
}

4、栈的典型应用
1. 就近匹配 （检测代码中括号是否成对出现）
当需要检测成对出现但又不相互邻近的事物时，可以使用“栈”的后进先出特性。
算法思路：
        从第一个字符开始扫描；
        当遇见普通字符时忽略；
        当遇见左符号时，压入栈中；
        当遇见右符号时，从栈中弹出栈顶元素，并进行匹配：
                匹配成功： 继续下一个字符；
                匹配失败：立即停止，并报错；
        结束：
                成功：所有字符扫描完毕，且栈为空；
                失败：匹配失败或所有字符串扫描完毕但栈非空。
2. 中缀 转 后缀
我们平时的数学表达式，如“1+2*3”，是把运算符放在中间，即中缀表达式，它符合人类的思考习惯，但并不适合计算机运算。
20世纪50年代波兰科学家提出了一种将运算符放在后面的后缀表达式。
后缀表达式：指的是不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，严格从左向右进行。
实例：
5 + 4   ==>  5 4 +
1 + 2 * 3  ==>  1 2 3 * +
8 + (3 - 1) * 5  ==> 8 3 1 - 5 * +
利用栈实现：中缀表达式  转换为  后缀表达式：
算法思路：
        逐个扫描中缀表达式中的数字和符号
        对于数字：  直接输出
        对于符号：
                左括号： 进栈
                运算符号：与栈顶符号进行优先级比较
                        若栈顶符号优先级低： 此符号进栈（默认左括号优先级最低）
                        若栈顶符号优先级不低：将栈顶符号弹出并输出，之后入栈
                右括号：将栈顶元素弹出并输出，直到匹配到左括号。
        遍历结束：将栈中所有符号弹出并输出。

3. 后缀表达式的计算
算法思路：
        遍历后缀表达式中的数字和符号
        对于数字：进栈
        对于符号：
                从栈中弹出左操作数
                从栈中弹出右操作数
                根据符号进行运算
                将运算结果压入栈中
        遍历结束：栈中唯一数字即为运算结果。

完整代码： 栈的顺序存储.zip (2.59 KB, 下载次数: 10)

2018-9-25 22:54 上传

点击文件名下载附件
栈的顺序存储

                栈的链式存储.zip (2.93 KB, 下载次数: 7)

2018-9-25 22:54 上传

点击文件名下载附件
栈的链式存储

                栈的典型应用.zip (4.5 KB, 下载次数: 8)

2018-9-25 22:54 上传

点击文件名下载附件
栈的典型应用