|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
本帖最后由 TCY 于 2021-2-14 13:48 编辑
sympy是一个Python的科学计算库,用一套强大的符号计算体系完成诸如多项式求值、求极限、解方程、求积分、微分方程、级数展开、矩阵运算等等计算问题。虽然Matlab的类似科学计算能力也很强大,但是Python以其语法简单、易上手、异常丰富的三方库生态,个人认为可以更优雅地解决日常遇到的各种计算问题。
如果你遇到了一个难题,不要犹豫,来找Python,它几乎不会让你失望的。
安装sympy库
常用的sympy内置符号
虚数单位i
- In [13]: import sympy
- In [14]: sympy.I
- Out[14]: I
- In [15]: sympy.I ** 2
- Out[15]: -1
- # 求-1的平方根
- In [16]: sympy.sqrt(-1)
- Out[16]: I
注:本文后面的示例都省略导包语句:import sympy
自然对数的底e
- In [18]: sympy.E
- Out[18]: E
- # 求对数
- In [20]: sympy.log(sympy.E)
- Out[20]: 1
无穷大oo
- In [26]: 1 / sympy.oo
- Out[26]: 0
- In [27]: 1 + sympy.oo
- Out[27]: oo
圆周率pi
- In [60]: sympy.pi
- Out[60]: pi
- In [61]: sympy.sin(sympy.pi / 2)
- Out[61]: 1
用sympy进行初等运算
Python 2.x中用除号/做两个整数的除法,实际上是整除运算,为了防止这种情况的发生,避免不必要的麻烦,下文的所有示例一开始都加上一句:from __future__ import division,这个时候除号/本身就变成了真实除法,而//才是整除,比如:
- # 导入division包之前
- In [1]: 1/2
- Out[1]: 0
- In [2]: from __future__ import division
- # 导入division包之后
- In [3]: 1/2
- Out[3]: 0.5
- In [4]: 1//2
- Out[4]: 0
求对数
- # 自然对数
- In [10]: sympy.log(sympy.E)
- Out[10]: 1
- In [11]: sympy.log(sympy.E ** 3)
- Out[11]: 3
- # 以10为底1000的对数
- In [12]: sympy.log(1000,10)
- Out[12]: 3
求平方根
- In [13]: sympy.sqrt(4)
- Out[13]: 2
- In [14]: sympy.sqrt(-1)
- Out[14]: I
求n次方根
- # 求8的3次方根
- In [15]: sympy.root(8,3)
- Out[15]: 2
求k次方
- In [21]: 2 ** 3
- Out[21]: 8
- In [22]: 16 ** (1 / 2)
- Out[22]: 4.0
求阶乘
- In [35]: sympy.factorial(4)
- Out[35]: 24
求三角函数
以sin函数为例:
- In [86]: sympy.sin(sympy.pi)
- Out[86]: 0
- In [87]: sympy.sin(sympy.pi / 2)
- Out[87]: 1
表达式与表达式求值
sympy可以用一套符号系统来表示一个表达式,如函数、多项式等,并且可以进行求值,比如:
- # 首先定义x为一个符号,表示一个变量
- In [96]: x = sympy.Symbol('x')
- In [97]: fx = 2 * x + 1
- # 可以看到fx是一个sympy.core.add.Add类型的对象,也就是一个表达式
- In [98]: type(fx)
- Out[98]: sympy.core.add.Add
- # 用evalf函数,传入变量的值,对表达式进行求值
- In [101]: fx.evalf(subs = {x : 2})
- Out[101]: 5.00000000000000
- In [102]: x,y = sympy.symbols('x y')
- In [103]: f = 2 * x + y
- # 以字典的形式传入多个变量的值
- In [104]: f.evalf(subs = {x : 1, y : 2})
- Out[104]: 4.00000000000000
- # 如果只传入一个变量的值,则原本输出原来的表达式
- In [105]: f.evalf(subs = {x : 1})
- Out[105]: 2.0*x + y
用sympy解方程(组)
使用sympy.solve函数解方程,该函数通常传入两个参数,第1个参数是方程的表达式(把方程所有的项移到等号的同一边形成的式子),第2个参数是方程中的未知数。函数的返回值是一个列表,代表方程的所有根(可能为复数根)。
解最简单的方程
比如下面我们来求两个方程:
- # 首先定义‘x’为一个符号,代表一个未知数
- In [24]: x = sympy.Symbol('x')
- # 解方程:x - 1 = 0
- In [25]: sympy.solve(x - 1, x)
- Out[25]: [1]
- # 解方程:x ^ 2 - 1 = 0
- In [26]: sympy.solve(x ** 2 - 1, x)
- Out[26]: [-1, 1]
- # 解方程:x ^ 2 + 1 = 0
- In [27]: sympy.solve(x ** 2 + 1, x)
- Out[27]: [-I, I]
把函数式赋给一个变量
有时候为了书写起来简洁,可以把一个函数式起个名字,比如:
- In [30]: x = sympy.Symbol('x')
- In [31]: f = x + 1
- In [32]: sympy.solve(f, x)
解方程组
比如要解这么个二元一次方程组:
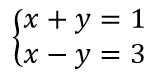
代码如下:
- # 一次性定义多个符号
- In [28]: x,y = sympy.symbols('x y')
- In [29]: sympy.solve([x + y - 1,x - y -3], [x, y])
- Out[29]: {x: 2, y: -1}
计算求和式
计算求和式可以使用sympy.summation函数,其函数原型为:sympy.summation(f, *symbols, **kwargs)。
话不多少,举个栗子,比如求下面这个求和式子的值:
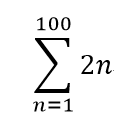
我们用初中的知识可以知道,这个式子的结果为:5050 * 2 = 10100
下面用代码来求:
- In [37]: n = sympy.Symbol('n')
- In [38]: sympy.summation(2 * n, (n, 1, 100))
- Out[38]: 10100
如果sympy.summation函数无法计算出具体的结果,那么会返回求和表达式。
解带有求和式的方程
比如求这么一个方程:
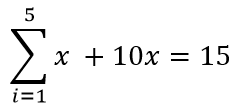
代码如下:
- In [43]: x = sympy.Symbol('x')
- In [44]: i = sympy.Symbol('i', integer = True)
- In [46]: f = sympy.summation(x, (i, 1, 5)) + 10 * x - 15
- In [47]: sympy.solve(f, x)
- Out[47]: [1]
求极限
求极限用sympy.limit函数,其函数文档如下:
- Signature: sympy.limit(e, z, z0, dir='+')
- Docstring:
- Compute the limit of e(z) at the point z0.
- z0 can be any expression, including oo and -oo.
- For dir="+" (default) it calculates the limit from the right
- (z->z0+) and for dir="-" the limit from the left (z->z0-). For infinite
- z0 (oo or -oo), the dir argument is determined from the direction
- of the infinity (i.e., dir="-" for oo).
如果学过微积分,就会知道微积分中有3个重要的极限:
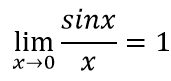
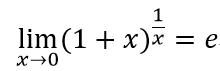
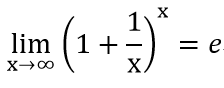
下面就用sympy.limit函数来分别求这3个极限:
- In [53]: x = sympy.Symbol('x')
- In [54]: f1 = sympy.sin(x)/x
- In [55]: sympy.limit(f1,x,0)
- Out[55]: 1
- In [56]: f2 = (1+x)**(1/x)
- In [57]: sympy.limit(f2,x,0)
- Out[57]: E
- In [58]: f3 = (1+1/x)**x
- In [59]: sympy.limit(f3,x,sympy.oo)
- Out[59]: E
求导
求导使用sympy.diff函数,传入2个参数:函数表达式和变量名,举例如下:
- In [63]: x = sympy.Symbol('x')
- In [64]: f = x ** 2 + 2 * x + 1
- In [65]: sympy.diff(f, x)
- Out[65]: 2*x + 2
- In [66]: f2 = sympy.sin(x)
- In [67]: sympy.diff(f2, x)
- Out[67]: cos(x)
- # 多元函数求偏导
- In [68]: y = sympy.Symbol('y')
- In [70]: f3 = x ** 2 + 2*x + y ** 3
- In [71]: sympy.diff(f3, x)
- Out[71]: 2*x + 2
- In [72]: sympy.diff(f3, y)
- Out[72]: 3 * y ** 2
求定积分
使用sympy.integrate函数求定积分,其功能比较复杂,非常强大,下面仅仅举几个比较简单的例子。
先来求一个最简单的积分:
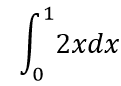
用牛顿-莱布尼兹公式可以立马口算出上面这个式子的结果是1,用代码计算如下:
- In [74]: x = sympy.Symbol('x')
- In [75]: f = 2 * x
- # 传入函数表达式和积分变量、积分下限、上限
- In [76]: sympy.integrate(f,(x,0,1))
- Out[76]: 1
下面来算一个复杂一点的多重积分:
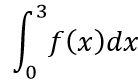
其中:
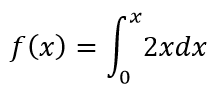
我们通过口算可以求出f(x):
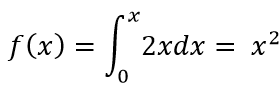
所以:
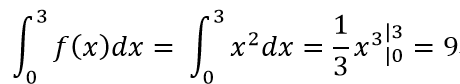
下面用代码来计算上述过程:
- In [82]: t,x = sympy.symbols('t x')
- In [83]: f = 2 * t
- In [84]: g = sympy.integrate(f,(t,0,x))
- In [85]: sympy.integrate(g,(x,0,3))
- Out[85]: 9
求不定积分
同样也是使用sympy.integrate函数求不定积分,下面仅仅举几个比较简单的例子。
比如求下面这个不定积分:
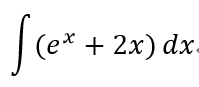
通过观察我们知道它的结果是:
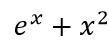
下面用代码来计算这个不定积分的结果:
- In [79]: x = sympy.Symbol('x')
- In [80]: f = sympy.E ** x + 2 * x
- In [81]: sympy.integrate(f,x)
- Out[81]: x**2 + exp(x)
总结
从上面的一系列计算可以看出,sympy是个非常强大的科学计算库,本文所讲到的用法仅仅是它强大功能的冰山一角,还需以后在实际使用中进一步发掘。
作者:m2fox
链接:https://www.jianshu.com/p/339c91ae9f41
来源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)