DEV C++ 快速排序的顺序坑

JCSY

最近重温算法知识，在快速排序算法一节，使用DEV C++编辑器编辑代码时遇到了编辑器发现bug报错的现象，折磨一番后，无奈翻出原先代码对比，发现仍无差错，想必或许是编辑器的问题，结果果真如此。。。

我只想静静的敲下代码，我乍地了*

此次重温算法时发现，大多数书籍对快速排序算法给出的代码如下：

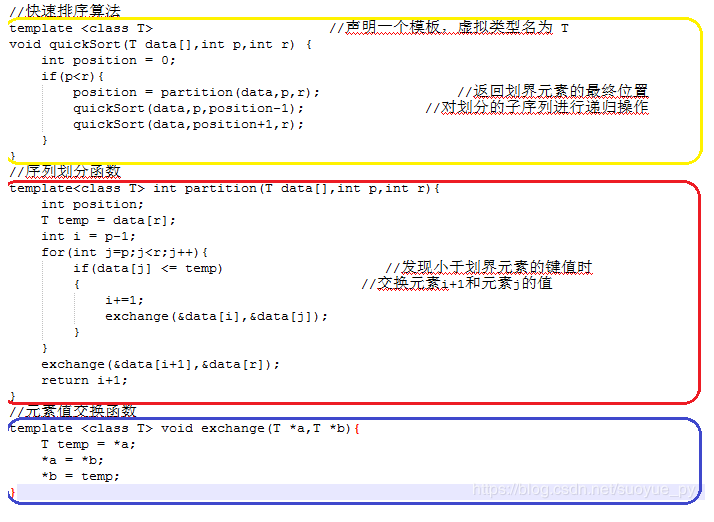
从上到下顺序：排序算法=>划分函数=>交换函数
对于visual C++编辑器来说是不会报错的，但使用DEV C++无法通过编译，编辑器会报错：



对此猜想报错的原因：代码块找不到不是因为没有定义，而是因为DEV C++的执行是模块化、有层次、有顺序的：从上到下（当然还是遵循主函数main()开始，这里的从上到下是指主函数的其他定义）。
对此修正代码：

修正方案一：
既然了解了原理，更换代码定义顺序即可：
交换函数=>划分函数=>排序算法
首先定义交换函数，划分函数需要调用交换函数故居其后，排序算法需要调用划分函数，亦居其后。
修正方案二：
在代码最前面进行声明：

快速排序算法的必看知识点：
原理：
取某个元素 v 作为待排序数组 S 的划界元素；
移动元素，将 剩下 的元素中小于或等于 v 的元素移动到 v 的前面划分为子序列 S1，将大于或等于 v 的元素移动到 v 的后面划分为子序列 S2 ；
返回 v 的位置，此时 v 就找到了其最终的排序位置；
递归地在子序列 S1 和 S2 上进行上述步骤，直到所有子序列都只包含 0 个或 1 个元素时听停止。
效率：
在通常情况下快速排序的效率较高，时间复杂度也较好，为O(nlong2n)，但若参加排序的元素原来就是有序的，这时快速排序的效率最低，时间复杂度为O(n2)。
注意：
快速排序是一个不稳定的排序算法。例如：在排序过程的最后一步，划界元素与元素 a 交换，若原数组中包含两个 a 元素，经过交换，则可能原本在前面的 a 值元素交换到了另一个同值元素的后面。

正确完整的源代码：（正确指：在visual C++和DEV C++均可正确运行）

// 快速排序算法实现   
#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

#define MAX 11
// 输入函数
void input(int num[]){
        int i;       
        srand((unsigned)time(NULL));        //设置随机种子
        for(i=1; i<MAX; i++)
                num=rand()%100;                        //生成随机函数
}
// 输出函数   
void output(int num[]){
        int i;       
        for(i=1; i<MAX; i++){
                cout<<num<<"  ";
                if(0 == i%10)
                        cout<<endl;
        }
        cout<<endl;
}
//元素值交换函数
template <class T>                                 //声明一个模板，虚拟类型名为 T
void exchange(T *a,T *b){
        T temp = *a;
        *a = *b;
        *b = temp;
}
//序列划分函数
template<class T>  int partition(T data[],int p,int r){
        int position;
        T temp = data[r];
        int i = p-1;
        for(int j=p;j<r;j++){
                if(data[j] <= temp)                    //发现小于划界元素的键值时
                {                                   //交换元素i+1和元素j的值
                        i+=1;
                        exchange(&data,&data[j]);
                }
        }
        exchange(&data[i+1],&data[r]);
        return i+1;
}
//快速排序算法
template <class T> void quickSort(T data[],int p,int r){
        int position = 0;
        if(p<r){
                position = partition(data,p,r);                         //返回划界元素的最终位置
                quickSort(data,p,position-1);                        //对划分的子序列进行递归操作
                quickSort(data,position+1,r);
        }
}

//主函数
int main(){
        int num[MAX];
        cout<<"快速排序前："<<endl;
        input(num);
        output(num);
        quickSort(num,0,10);
        cout<<"快速排序后："<<endl;
        output(num);
        return 0;
}

---------------------
作者：《~锁钥~》
来源：CSDN
原文：https://blog.csdn.net/suoyue_py/article/details/96100936
版权声明：本文为博主原创文章，转载请附上博文链接！