[已解决]Python：每日一题 306

zltzlt

今天的题目：

将一个连分数化成最简分数。



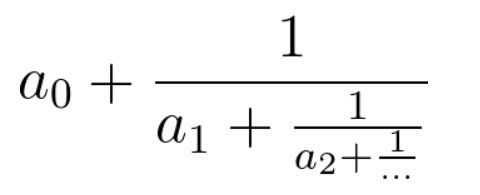
连分数是形如上图的分式。在本题中，所有系数都是大于等于 0 的整数。

输入的 cont 代表连分数的系数（cont[0] 代表上图的 a0，以此类推）。
返回一个长度为 2 的数组 [n, m]，使得连分数的值等于 n / m，且 n、m 最大公约数为 1。

示例 1：

输入：cont = [3, 2, 0, 2]
输出：[13, 4]
解释：原连分数等价于 3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意 [26, 8]、[-13, -4] 都不是正确答案。

示例 2：

输入：cont = [0, 0, 3]
输出：[3, 1]
解释：如果答案是整数，令分母为 1 即可。

欢迎大家一起答题！

最佳答案

月排行榜 / 总排行榜

阴阳神万物主

2020-1-16 00:30:27

感觉解法都大同小异呢。

1. def solve(cont:'list of int >= 0')->'[n,m]':
   
2.     res = [0,1]
   
3.     for each in cont[:0:-1]:
   
4.         res[0],res[1] = res[1],each*res[1]+res[0]
   
5.     else:
   
6.         res[0],res[1] = cont[0]*res[1]+res[0],res[1]
   
7.     def gcd(a,b):
   
8.         while a!=b and a and b:
   
9.             a,b = b%a,a
   
10.         return a or b
    
11.     n=gcd(res[0],res[1])
    
12.     return res
    
13. if __name__ == '__main__':
    
14.     print('示例1 输出：',solve([3, 2, 0, 2]))
    
15.     print('示例2 输出：',solve([0, 0, 3]))
    

复制代码

跳转到最佳答案楼层

Croper

话说几天前才说到过这个问题。。。
连分数拿来小数划分数很有用

1. def func306(l:list):
   
2.     num,den=0,1
   
3.     for i in reversed(l):
   
4.         num,den=den,num+i*den;
   
5.     a,b=num,den
   
6.     while (b!=0):
   
7.         a,b=b,a%b
   
8.     num//=a
   
9.     den//=a
   
10.    #if (num<0):  //系数大于等于0？ 那这一句不需要了
    
11.         #num=-num
    
12.         #den=-den
    
13.     return [den,num]
    

复制代码

塔利班

1. def f306(cont):
   
2.     m,z=1,0
   
3.     for e in cont[::-1]:
   
4.         m,z=e*m+z,m
   
5.     x,y=m,z
   
6.     while y:
   
7.         x,y=y,x%y
   
8.     if z<0:
   
9.         x=-1
   
10.     z=z//x
    
11.     m=m//x
    
12.     return [m,z]

复制代码

如有一个﹣号是给分母吧

sunrise085

我用的是递归。
我有个疑问，这个会有不是最简分数的情况吗？每次向外层走，都是一个最简分数加一个整数，仍然是最简分数啊。也不会出现负数的情况吧？不过在程序中还是写了这一部分~~

1. def fun306(list1):
   
2.     if len(list1)==2:
   
3.         numerator = list1[0] * list1[1] + 1
   
4.         denominator = list1[1]
   
5.     else:
   
6.         [nume,deno] = fun306(list1[1:])
   
7.         numerator = list1[0] * nume + deno
   
8.         denominator = nume
   
9.     a,b=numerator,denominator
   
10.     while (b != 0):
    
11.         a,b = b,a%b
    
12.     numerator //= a
    
13.     denominator //= a
    
14.     if numerator < 0:
    
15.         numerator = -numerator
    
16.         denominator = -denominator        
    
17.     return [numerator,denominator]
    
18. 
    
19. list1=[3,2,0,2]
    
20. print(fun306(list1))

复制代码

冬雪雪冬

1. from fractions import Fraction
   
2. from functools import reduce
   
3. def fun(cont):
   
4.     result =  reduce(lambda x, y: y + Fraction(1, x), cont[::-1])
   
5.     return [result.numerator, result.denominator]

复制代码

阴阳神万物主

塔利班 发表于 2020-1-15 21:58
如有一个﹣号是给分母吧

题目交代了，没有负数呀。

阴阳神万物主

感觉解法都大同小异呢。

1. def solve(cont:'list of int >= 0')->'[n,m]':
   
2.     res = [0,1]
   
3.     for each in cont[:0:-1]:
   
4.         res[0],res[1] = res[1],each*res[1]+res[0]
   
5.     else:
   
6.         res[0],res[1] = cont[0]*res[1]+res[0],res[1]
   
7.     def gcd(a,b):
   
8.         while a!=b and a and b:
   
9.             a,b = b%a,a
   
10.         return a or b
    
11.     n=gcd(res[0],res[1])
    
12.     return res
    
13. if __name__ == '__main__':
    
14.     print('示例1 输出：',solve([3, 2, 0, 2]))
    
15.     print('示例2 输出：',solve([0, 0, 3]))
    

复制代码

zltzlt

sunrise085 发表于 2020-1-15 22:05
我用的是递归。
我有个疑问，这个会有不是最简分数的情况吗？每次向外层走，都是一个最简分数加一个整数， ...

[nume,deno] = haha(list1[1:])

haha 是什么？

sunrise085

zltzlt 发表于 2020-1-16 09:25
[nume,deno] = haha(list1[1:])

haha 是什么？

呃，写程序的时候起的函数名，忘记修改了，递归，这里是fun306，现在已经修改

zltzlt

sunrise085 发表于 2020-1-15 22:05
我用的是递归。
我有个疑问，这个会有不是最简分数的情况吗？每次向外层走，都是一个最简分数加一个整数， ...

超出递归最大深度

kinkon

1. def f306(cont):
   
2.     cont = cont[::-1]
   
3.     ncont = [0,1]
   
4.     while len(cont) > 0:
   
5.         ncont[0], ncont[1] = ncont[1], ncont[0]+cont[0]*ncont[1]
   
6.         del cont[0]
   
7.     return ncont[::-1]

复制代码

TJBEST

1. def fun306new(cont):
   
2.     def add(p,q):#p是既约分数[分子，分母],q是整数 既约分数加整数的通分仍既约 根本不用化简 数论知识就是好！
   
3.         m = p[0] + p[1]*q
   
4.         n = p[1]
   
5.         return [m,n]
   
6.     def dao(w):#倒数
   
7.         return list(reversed(w))
   
8. #因为连分数合法 所以最后1个数不能是零
   
9.     n = len(cont) - 1
   
10.     res = [cont[n],1]
    
11.     if n == 0:
    
12.         return res
    
13.     for each in cont[(n-1)::-1]:
    
14.         res = add(dao(res),each)
    
15.     return res

复制代码

fan1993423

1. from functools import reduce
   
2. from fractions import Fraction
   
3. def fun306(cont):
   
4.     if not len(cont):return 0
   
5.     cont_reverse=reversed(cont)
   
6.     try:
   
7.         num=reduce(lambda x,y:Fraction(1/x+y),cont_reverse)
   
8.         return list(map(int,str(num).split('/')))
   
9.     except ZeroDivisionError:
   
10.         return '分母不能为0，计算结果错误'

复制代码

zltzlt

fan1993423 发表于 2020-1-16 16:10

解答错误

输入：[0, 0, 3]
输出：[18014398509481984, 6004799503160661]
预期结果：[3, 1]

fan1993423

zltzlt 发表于 2020-1-16 16:22
解答错误

输入：[0, 0, 3]

它这个是python的精度问题，不是我程序的问题

zltzlt

fan1993423 发表于 2020-1-16 16:35
它这个是python的精度问题，不是我程序的问题

是，但你要改

fan1993423

这样吧，我稍微改一下

1. from functools import reduce
   
2. from fractions import Fraction
   
3. def fun306(cont):
   
4.     if not len(cont):return 0
   
5.     cont_reverse=reversed(cont)
   
6.     try:
   
7.         num=reduce(lambda x,y:Fraction(1,x)+y,cont_reverse)
   
8.         d=list(map(int,str(num).split('/')))
   
9.         return d if len(d)==2 else d+[1]
   
10.     except ZeroDivisionError:
    
11.         return '分母不能为0，计算结果错误'

复制代码

wanting-for

1. list1 = list(map(int,input().split()))
   
2. list1.reverse()
   
3. ncont = [list1[0],1]
   
4. while len(list1)>0:
   
5.     del list1[0]
   
6.     if len(list1) == 0:
   
7.         break
   
8.     else:
   
9.         ncont.reverse()
   
10.         ncont[0],ncont[1] = ncont[0]+ncont[1]*list1[0],ncont[1]
    
11. print(ncont)
    
12.    
    
13.         
    

复制代码

#膜拜大佬，看完大佬的代码才知自己还需要很长时间的努力！
#列表表示分数，实在漂亮！