|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
枚举算法
枚举算法就是按照问题本身的性质,一一列举出该问题所有的解,并根据问题的条件对各解进行逐个检验,从中挑选出符合条件的解,舍弃不符合条件的解。
枚举算法的思路
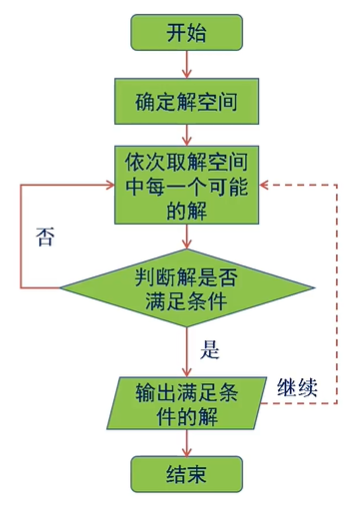
枚举算法举例
例 1
求 1 ~ 1000 中,能被 7 和 11 同时整除的数。
输出为两行,第一行为所有满足题目要求的数,以空格分割;第二行为满足题目要求的数的个数。
程序如下:
- #include <iostream>
- using namespace std;
- int main()
- {
- int i, count = 0;
- for (i = 1; i <= 1000; i++)
- {
- if (i % 7 == 0 && i % 11 == 0)
- {
- cout << i << " ";
- count++;
- }
- }
- cout << endl;
- cout << count;
- return 0;
- }
执行结果:
- 77 154 231 308 385 462 539 616 693 770 847 924
- 12
例 2
求 100 ~ 999 中的所有水仙花数。
第一行为所有满足题目要求的数,以空格分割;第二行为所有满足题目要求的数的个数。
程序如下:
- // 求水仙花数
- #include <iostream>
- using namespace std;
- int main()
- {
- int i, count = 0, a, b, c;
- for (i = 100; i < 1000; i++)
- {
- a = i / 100;
- b = i % 100 / 10;
- c = i % 10;
- if ((a * a * a + b * b * b + c * c * c) == i)
- {
- cout << i << " ";
- count++;
- }
- }
- cout << endl;
- cout << count;
- return 0;
- }
执行结果:
枚举算法总结
优点:比较直观,容易理解;正确性容易证明。
不足:效率低
枚举算法是最简单、最直白、最粗暴的方法,它根据所需解决问题的条件,把该问题所有的解全部列举出来,并逐个检验出问题真正的解。
枚举算法又被称为穷举算法。 |
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)