|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
图的遍历
同树结构一样,图结构也有遍历操作,即从某个顶点出发,沿着某条路径对其余顶点进行访问,且使每个顶点均被访问一次。
但图的遍历要比树的遍历更复杂,因为图中可能存在回路,所以在访问了某个顶点之后,可能沿着某条回路又回到了该顶点。
为了避免同一顶点被重复访问,则在遍历过程中,必须为已经访问过的顶点加上标识,使其不再重复被访问。
在遍历过程中,通常需附设一维数组 visited[n],令其每个分量对应图中的一个顶点,各分量的初值均设置为 0 。
一旦访问了某个顶点,便将 visited 中相应分量的值置为 true 或被访问时的序号。
通常对图进行遍历有两种遍历方法:深度优先遍历和广度优先遍历。
深度优先遍历 DFS
深度优先遍历类似于树的先序遍历,可以看成是先序遍历的推广。
假设初始状态是图中的顶点均未被访问,则从某个顶点 v 出发。
首先访问该顶点,然后依次从它的各个未被访问的邻接点出发,深度优先遍历图,直至图中所有和 v 有路径相通的顶点都被访问到。
可以看出,深度优先遍历是一个递归的过程。
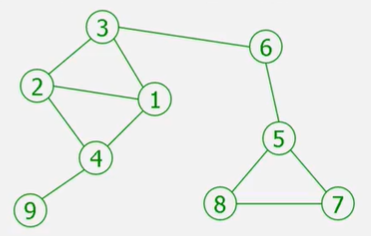
例如从顶点 3 开始对上图进行深度优先遍历。
首先访问顶点 3,然后从顶点 3 的邻接点 2 出发进行深度优先遍历,先后访问顶点 4、9、1。
由于顶点 3 的第二个邻接点 1 已经被访问过,则不再从顶点 1 出发进行遍历。
而顶点 3 的下一个邻接点 6 未被访问,则再从顶点 6 出发遍历。
接下来依次遍历顶点 5 、8 、7 。
所以最后遍历过程中访问顶点的次序是:3 2 4 9 1 6 5 8 7 。
广度优先遍历 BFS
广度优先遍历的基本思想是:
从图中某顶点 v 出发,在访问了 v 之后依次访问 v 的各个未曾访问过的邻接点。
然后分别从这些邻接点出发,依次访问它们的邻接点,并使得 “先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问” 。
换句话说,广度优先遍历的过程是以顶点 v 为起点,由近至远,依次访问和顶点 v 有路径相通且路径长度为 1, 2, ... 的顶点。
“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问” —— 顺序访问,需要队列来完成。 |
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)