19年安徽省赛G. 括号序列

MFwxy

G. 括号序列

描述
  括号序列是指由‘(’和‘)’组成的序列，假如一个括号序列中，包含相同数量的左括 号和右括号，并且对于每一个右括号，在他的左侧都有左括号和他匹配，则这个 括号序列就是一个合法括号序列。比如(())()就是一个合法括号序列，但 (())(()不是合法括号序列。
给出两个长度相同的合法括号序列A 和B，那么A < B当且仅当：
&#61548; A 和B至少有一位不相同。
&#61548; 在A 和B从左往右数第一个不相同的位置i，A[i]=(，B[i]=)

比如A = (())()，B = ()()()，则A < B，因为从左边数第一个不相同的 是第二个字符，A[2] = (,B[2] = )。对于长度 N，由于定义了小于关系， 则可以通过这个关系推出所有长度为 N 的合法括号序列的大小关系，对于长度 为6的合法括号序列，从小到大排列顺序如下：
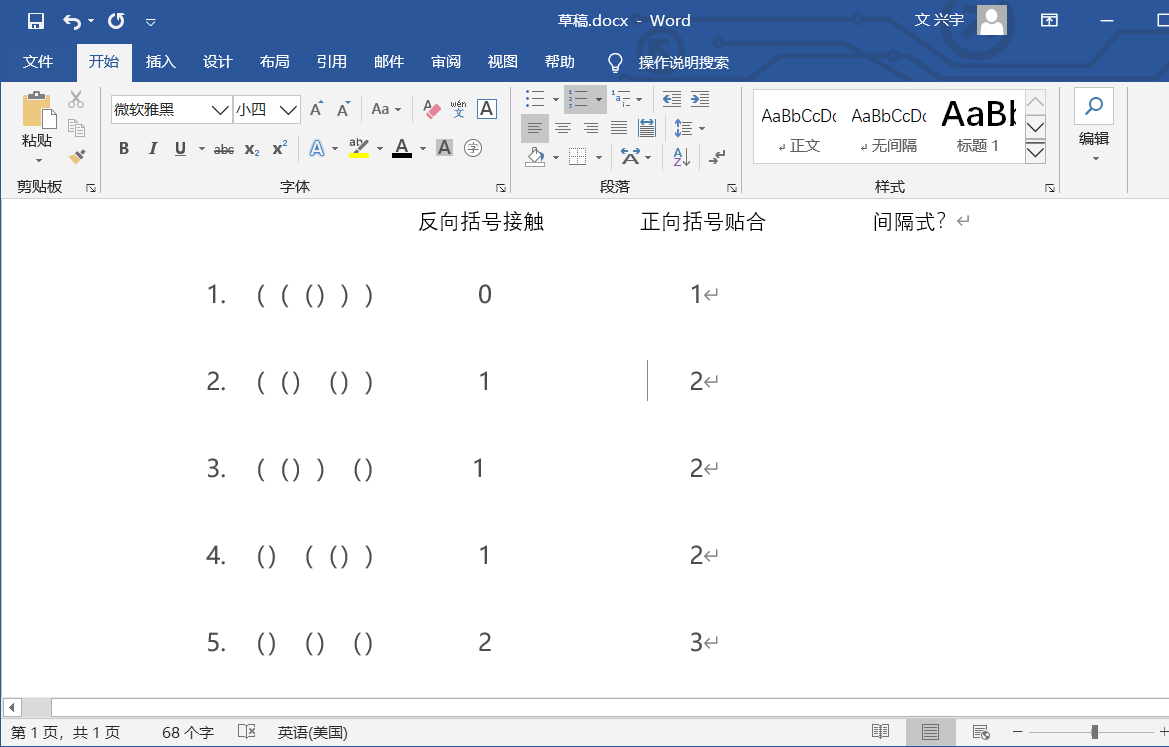
1.((()))
2.(()())
3.(())()
4.()(())
5.()()()
给出N和M，求长度为N的合法括号序列中，第M 小的合法括号序列是？

输入
输入的第一行是N 和M
2 <= N <= 2000
1 <= M <= 10^18

输出格式
输出一个字符串，表示长度为N的平衡括号序列从小到大排列，序号为M的字符串

样例输入
6 2
样例输出
(()())

解：。。。
一开始的思路是投机倒把（确实方便理解，但是效果不明显，不呈现了）
想把右括号根据它所在位置数字化，的确能做到给定括号序列判断他们的正确性以及大小，但是反向输出好像有点难。。。就放弃了
然后想通过左右括号交错的位置来整活，好像结果也不是很理想。

然后正常的去考虑动态规划。
大佬指点：
a：
dp算下吧
算出每个长度的括号序列有多少个
然后一个一个就推出来了
超过1e18就扔了
当做正无穷
因为只问前1e18项
反正后面也不算简单
大概就是看看最前面能放几个左括号
反正就是要算每一步怎么走
走完之后还要找多少个比这个小的路径
可能记忆化搜索更好写
也可以算我说的那个加组合数
差不多吧
记忆化搜索慢点儿
不过这个无所谓
b：
n^2dp
看看當前選（幾種路,）幾種路
你可以想成是對角線下的路徑
要在爆long long前變成inf

c：
括号这个好像是Catalan数

dp数组是什么？
动态规划是通过找当前项和前一或几项或后一或几项的关系,从而对一个数组多次利用达到减少复杂度。
1.当一串数可以不限次利用时，采用顺序的方式循环：for(j=0;j<=max_n;j++)（一维数组）或者加一个for(k=0;k*A[i]<=j;k++)(二维数组)
2.当一串数的使用次数有限时用for(k=0;k*A[i]<=j&&k<=B[i];k++)(二维数组)
3.当一串数的使用次数为一时，用倒序的方式循环：for(j=max_n;j>=0;j–)(一维数组),或者for(j=0;j<=max_n;j++)(二维数组)；或者另外开一个一维数组，用来每i一次就记录一次这个数组，格式一次前一个数组。

其实应该可以说明之前的树形图递归生成的想法是有可行性的

继续扒一扒dp算法和卡特兰数。。


大致结果：

1. #include <iostream>
   
2. #include<algorithm>
   
3. 
   
4. using namespace std;
   
5. typedef long long ll;
   
6. 
   
7. const int N = 2010;
   
8. int n;
   
9. ll f[N][N], k;
   
10. char ans[N];
    
11. 
    
12. int main() {
    
13.         cin>>n>>k;
    
14. 
    
15. 
    
16. 
    
17.         f[0][0] = 1;
    
18.         ll INF = 1e18 + 10;
    
19.         for (int i = 1; i <= n; ++i)
    
20.                 for (int j = 0; j <= n; ++j) if (f[i - 1][j]) {               
    
21.                         f[i][j + 1] += f[i - 1][j];
    
22.                         f[i][j + 1] = min(f[i][j + 1], INF);
    
23.                         for (int j = 0; j < n; j++)
    
24.                         {
    
25.                                 for (int i = 0; i < n; i++)
    
26.                                 {
    
27.                                         cout << f[i][n - j] << " ";
    
28.                                 }
    
29.                                 cout << endl;
    
30.                         }
    
31.                         if (j) f[i][j - 1] += f[i - 1][j];
    
32.                         if (j) f[i][j - 1] = min(f[i][j - 1], INF);
    
33.                         cout << endl;
    
34.                         for (int j = 0; j < n; j++)
    
35.                         {
    
36.                                 for (int i = 0; i < n; i++)
    
37.                                 {
    
38.                                         cout << f[i][n - j] << " ";
    
39.                                 }
    
40.                                 cout << endl;
    
41.                         }
    
42.                         cout << endl;
    
43.         }
    
44.         int n2 = 0;
    
45.         cout << endl;
    
46.         for (int j = 0; j < n; j++)
    
47.         {
    
48.                 for (int i = 0; i < n; i++)
    
49.                 {
    
50.                         cout << f[i][n-j]<<" ";
    
51.                 }
    
52.                 cout << endl;
    
53.         }
    
54.         for (int i = 1; i <= n; ++i) {
    
55.                 if (f[n - i][n2 + 1] >= k)
    
56.                         ans[i] = '(', ++n2;
    
57.                 else
    
58.                         ans[i] = ')', k -= f[n - i][n2 + 1], --n2;
    
59.         }
    
60.         puts(ans + 1);
    
61. }

复制代码

VS2017
括号变换原理还是不太懂

赚小钱

TL;DR