|
|
10鱼币
有个微分方程要用龙格-库塔法求解,但我编程求解后的图和实际的图不一样,是否有了解的鱼油看看问题所在?多谢!!!
1. 原微分方程:
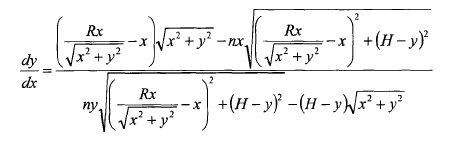
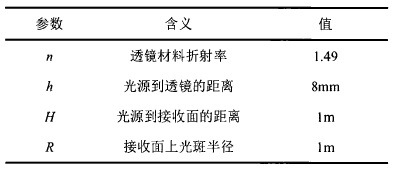
2.边界条件:(其中,h=8mm,理解为当x=0时,y=8)
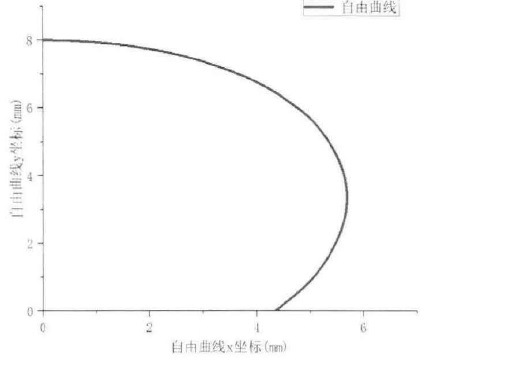
3.别人用Matlab编程得到的曲线图:
4.我用Python编写的程序及对应的曲线图:
- import numpy as np
- import matplotlib.pyplot as plt
- # 龙格-库塔法函数定义
- def runge_kutta(y, x, dx, f):
- """ y is the initial value for y
- x is the initial value for x
- dx is the time step in x
- f is derivative of function y(t)
- """
- k1 = dx * f(y, t)
- k2 = dx * f(y + 0.5 * k1, x + 0.5 * dx)
- k3 = dx * f(y + 0.5 * k2, x + 0.5 * dx)
- k4 = dx * f(y + k3, x + dx)
- return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6.
- if __name__=='__main__':
- t = 0.0
- y = 8.0 # 初始值为(0,8)
- dt = 0.000001 #步长
- ys, ts = [], []
- # 微分方程函数定义
- def func(y, t):
- v1 = np.sqrt(t**2 + y**2)
- v2 = 1000 * t / v1
- v3 = np.sqrt((v2 - t)**2 + (1000 - y)**2)
- return (v1*(v2-t)-1.49*t*v3)/(1.49*y*v3-(1000-y)*v1)
-
- while t <= 6: # 迭代边界条件
- y = runge_kutta(y, t, dt, func)
- t += dt
- ys.append(y)
- ts.append(t)
- plt.plot(ts, ys, label='runge_kutta')
- plt.legend()
- plt.show()
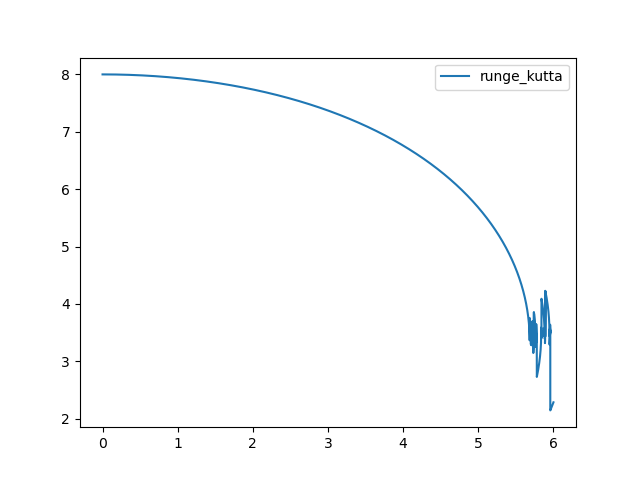
matlab的图中一个x值对应两个y值,但是你写的函数runge_kutta返回值只有一个,所以一个x对应的是一个y值,肯定就跟matlab图不一样了
|
最佳答案
查看完整内容
matlab的图中一个x值对应两个y值,但是你写的函数runge_kutta返回值只有一个,所以一个x对应的是一个y值,肯定就跟matlab图不一样了
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)