Leetcode 994. Rotting Oranges

Seawolf

1. In a given grid, each cell can have one of three values:
   
2. 
   
3. the value 0 representing an empty cell;
   
4. the value 1 representing a fresh orange;
   
5. the value 2 representing a rotten orange.
   
6. Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten.
   
7. 
   
8. Return the minimum number of minutes that must elapse until no cell has a fresh orange.  If this is impossible, return -1 instead.
   
9. 
   
10. 
    
11. 
    
12. Example 1:
    
13. 
    
14. 
    
15. 
    
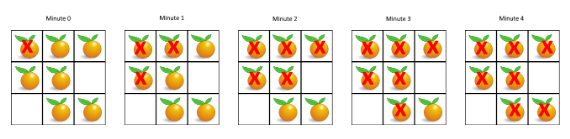
16. Input: [[2,1,1],[1,1,0],[0,1,1]]
    
17. Output: 4
    
18. Example 2:
    
19. 
    
20. Input: [[2,1,1],[0,1,1],[1,0,1]]
    
21. Output: -1
    
22. Explanation:  The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
    
23. Example 3:
    
24. 
    
25. Input: [[0,2]]
    
26. Output: 0
    
27. Explanation:  Since there are already no fresh oranges at minute 0, the answer is just 0.
    
28. 
    
29. 
    
30. Note:
    
31. 
    
32. 1 <= grid.length <= 10
    
33. 1 <= grid[0].length <= 10
    
34. grid[i][j] is only 0, 1, or 2.

复制代码

1. class Solution:
   
2.     def orangesRotting(self, grid: List[List[int]]) -> int:
   
3.         directions = [[1, 0], [-1, 0], [0, 1], [0, -1]]
   
4.         queue = []
   
5.         visited = set()
   
6.         m = len(grid)
   
7.         n = len(grid[0])
   
8.         level = 0
   
9.         count = 0
   
10.         goal = 0
    
11.         c = 0
    
12.         
    
13.         for i in range(m):
    
14.             for j in range(n):
    
15.                 if grid[i][j] == 2:
    
16.                     queue.append([i, j])
    
17.                     visited.add((i, j))
    
18.                     count += 1
    
19.                     goal += 1
    
20.                 if grid[i][j] == 1:
    
21.                     count += 1
    
22.                     c += 1
    
23.         if c == 0:
    
24.             return 0
    
25.         while queue:
    
26.             size = len(queue)
    
27.             
    
28.             for i in range(size):
    
29.                 cur = queue.pop(0)
    
30.                 x = cur[0]
    
31.                 y = cur[1]
    
32.                
    
33.                 for direction in directions:
    
34.                     new_x = x + direction[0]
    
35.                     new_y = y + direction[1]
    
36.                     if new_x < 0 or new_x >= m or new_y < 0 or new_y >= n or grid[new_x][new_y] == 0 or (new_x, new_y) in visited:
    
37.                         continue
    
38.                     
    
39.                     if grid[new_x][new_y] == 1 and (new_x, new_y) not in visited:
    
40.                         goal += 1
    
41.                         grid[new_x][new_y] = 2
    
42.                         queue.append([new_x, new_y])
    
43.                         visited.add((new_x, new_y))
    
44.             level += 1
    
45.             if goal == count:
    
46.                 return level
    
47.         
    
48.         for i in range(m):
    
49.             for j in range(n):
    
50.                 if grid[i][j] == 1:
    
51.                     return -1
    
52.         return level
    
53.             

复制代码