Leetcode 1536. Minimum Swaps to Arrange a Binary Grid

Seawolf

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

 

Example 1:








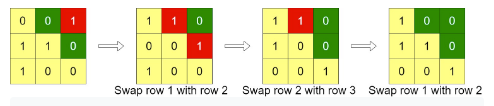
Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3
Example 2:








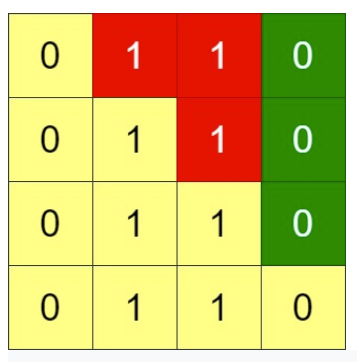
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.
Example 3:








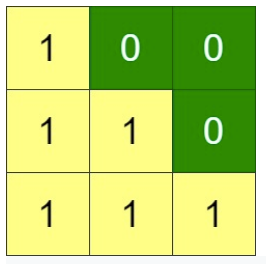
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0
 

Constraints:

n == grid.length
n == grid[i].length
1 <= n <= 200
grid[i][j] is 0 or 1

class Solution:
    def minSwaps(self, grid: List[List[int]]) -> int:
        zeros = [0 for _ in grid]
        result = 0
        for i in range(len(grid)):
            count = 0
            for j in range(len(grid[i]) - 1, -1, -1):
                if grid[i][j] != 0:
                    break
                count += 1
            zeros[i] = count
        
        n = len(grid)
        for i in range(len(grid)):
            target = n - i - 1
            for j in range(i, len(grid) + 1):
                
                if j < n and zeros[j] >= target:
                    break
            if j == n:
                return -1
            result += j - i
            temp = zeros[j]
            for k in range(j, i, -1):
                zeros[k] = zeros[k - 1]
            zeros[i] = temp
        return result