Leetcode 1584. Min Cost to Connect All Points

Seawolf

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.



Example 1:



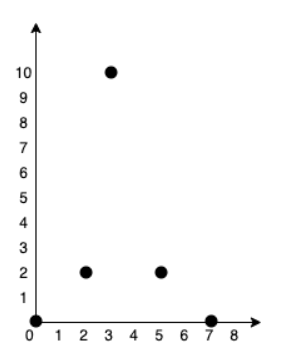
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation:



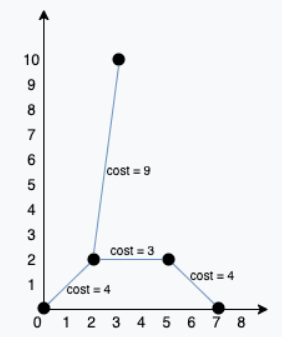
We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.
Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18
Example 3:

Input: points = [[0,0],[1,1],[1,0],[-1,1]]
Output: 4
Example 4:

Input: points = [[-1000000,-1000000],[1000000,1000000]]
Output: 4000000
Example 5:

Input: points = [[0,0]]
Output: 0


Constraints:

1 <= points.length <= 1000
-106 <= xi, yi <= 106
All pairs (xi, yi) are distinct.

class UnionFind:
    def __init__(self, n: int):
        self.parent = list(range(n))
        self.size = [1] * n
        
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    
    def union(self, x, y):
        rx, ry = self.find(x), self.find(y)
        if rx == ry: return False
        
        if self.size[rx] < self.size[ry]:
            rx, ry = ry, rx
            
        self.parent[ry] = rx
        self.size[rx] += self.size[ry]
        
        return True
        
class Solution:
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        N = len(points)
        edges = []
        res = 0
        
        for i in range(N):
            for j in range(i + 1, N):
                distance = abs(points[i][0] - points[j][0])
                distance += abs(points[i][1] - points[j][1])
                
                edges.append((distance, i, j))
        
        edges.sort()
        
        unionfind = UnionFind(N)
        
        for edge in edges:
            dis, i, j = edge
            if unionfind.union(i, j):
                res += dis
            
        return res