[已解决]BUG 求解！！！ 回帖一鱼币 ^__^

八戒253

1. #include <stdio.h>
   
2. #include <stdbool.h>
   
3. int main(void)
   
4. {
   
5.         bool flag = false;
   
6.         int su_shu[1000];
   
7.         int N,i,j,k=1;
   
8.         int count = 0;//用来记录最后的数
   
9.         scanf("%d",&N);
   
10.     if(N!=1)
    
11.         su_shu[0] = 2;
    
12.         for(i=3;i<=N;i++)
    
13.         {
    
14.                 for(j=2;j<i;j++)
    
15.                 {
    
16.                         if(i%j == 0)
    
17.                         {
    
18.                                 flag = true;
    
19.                                 break;
    
20.                         }
    
21.                 }
    
22.                 if(!flag)
    
23.                 {
    
24.                         su_shu[k++] = i;
    
25.                 }
    
26.                 flag = false;
    
27.         }
    
28.                
    
29.         for(i=0;i<k-1;i++)
    
30.         {
    
31.                 if(su_shu[i+1]-su_shu[i]==2)
    
32.                 {
    
33.                         count++;
    
34.                 }
    
35.         }
    
36.         printf("%d",count);
    
37.         return 0;
    
38. }

复制代码

PTA

让我们定义d&#8203;n&#8203;&#8203;为：d&#8203;n&#8203;&#8203;=p&#8203;n+1&#8203;&#8203;&#8722;p&#8203;n&#8203;&#8203;，其中p&#8203;i&#8203;&#8203;是第i个素数。显然有d&#8203;1&#8203;&#8203;=1，且对于n>1有d&#8203;n&#8203;&#8203;是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。

现给定任意正整数N(<)，请计算不超过N的满足猜想的素数对的个数。

输入格式:

输入在一行给出正整数N。

输出格式:

在一行中输出不超过N的满足猜想的素数对的个数。

输入样例:20

输出样例:4 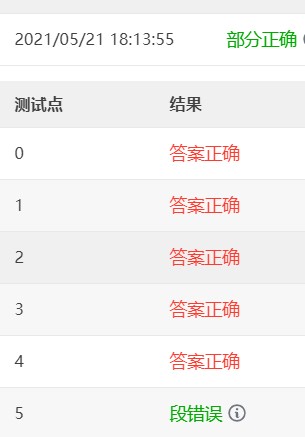该如何解决？？感谢帮助！！！

最佳答案

月排行榜 / 总排行榜

ba21

2021-5-21 20:03:40

八戒253 发表于 2021-5-21 19:36
我在下面跟帖的图片就是的啦

1. #include<stdio.h>
   
2. #include<math.h>
   
3. 
   
4. int IsPrime(int n) // 判断素数的函数
   
5. {
   
6.         int i;
   
7.         for(i=2;i<=sqrt(n);i++) // 高效求素数的范围 i<=sqrt(n)
   
8.         {
   
9.                 if(n%i==0)
   
10.                         return 0;
    
11.         }
    
12.         return 1;
    
13. }
    
14. 
    
15. int main()
    
16. {
    
17.         int N;
    
18.         scanf("%d",&N);
    
19.     if( N>0 && N<(int)pow(10, 5) )
    
20.     {
    
21.         int i, count=0; // const 用来记录"相邻且差为2的素数"的个数
    
22.         for(i=3;i<=N-2;i+=2) // 每组的跨度
    
23.         {
    
24.             if( IsPrime(i)&&IsPrime(i+2) ) // 相邻且差为2的素数
    
25.                 count++;
    
26.          }
    
27.         printf("%d\n",count);
    
28.     }
    
29. 
    
30. 
    
31.         return 0;
    
32. }
    

复制代码

跳转到最佳答案楼层

八戒253

ba21

PTA说什么？

八戒253

ba21 发表于 2021-5-21 19:35
PTA说什么？

我在下面跟帖的图片就是的啦

王之叹息

鱼币鱼币，虽然我不会

ba21

八戒253 发表于 2021-5-21 19:36
我在下面跟帖的图片就是的啦

1. #include<stdio.h>
   
2. #include<math.h>
   
3. 
   
4. int IsPrime(int n) // 判断素数的函数
   
5. {
   
6.         int i;
   
7.         for(i=2;i<=sqrt(n);i++) // 高效求素数的范围 i<=sqrt(n)
   
8.         {
   
9.                 if(n%i==0)
   
10.                         return 0;
    
11.         }
    
12.         return 1;
    
13. }
    
14. 
    
15. int main()
    
16. {
    
17.         int N;
    
18.         scanf("%d",&N);
    
19.     if( N>0 && N<(int)pow(10, 5) )
    
20.     {
    
21.         int i, count=0; // const 用来记录"相邻且差为2的素数"的个数
    
22.         for(i=3;i<=N-2;i+=2) // 每组的跨度
    
23.         {
    
24.             if( IsPrime(i)&&IsPrime(i+2) ) // 相邻且差为2的素数
    
25.                 count++;
    
26.          }
    
27.         printf("%d\n",count);
    
28.     }
    
29. 
    
30. 
    
31.         return 0;
    
32. }
    

复制代码

划句顾

ilovepython!

py还是c\c++还是java什么的？（首先排除py）

zenghaiaaa

谢谢楼主

tigerPython2019