34 - 二叉树的奥义：堆排序

鱼C-小师妹

在线讲解：

                               
登录/注册后可看大图

在开始介绍堆排序前，我们先介绍下什么是二叉树。

二叉树（Binary Tree）是包含 n 个节点的有限集合，该集合或者为空集（此时，二叉树称为空树）。

或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。

最简单的样子：



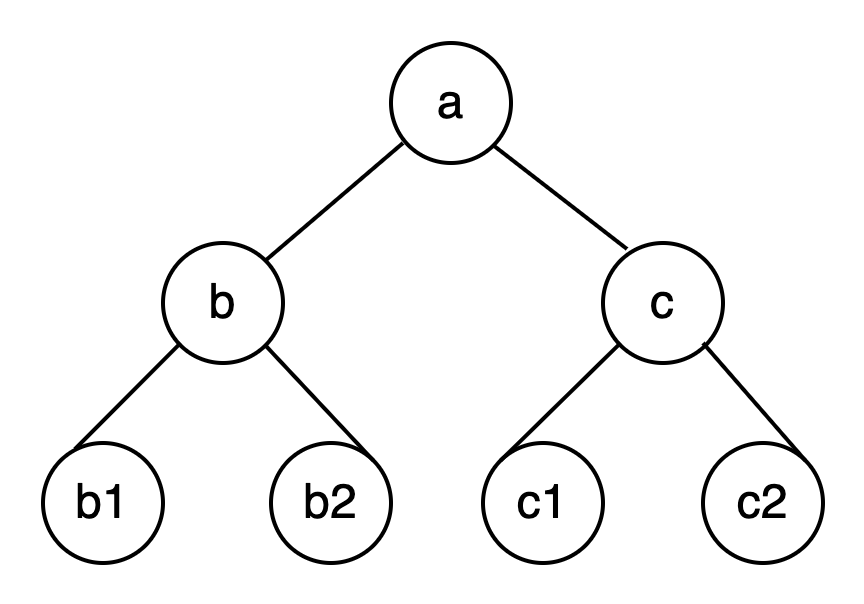
从上面的定义，不知道童鞋们有没有发现：

二叉树其实是一种递归的定义。

也可用递归形式给出：

一个二叉树是 n 个节点的集合，此集合要么是空集，要么是由一个根节点加上分别称为左子树和右子树的两个互不相交的二叉树组成。

由上述定义可知：

• 二叉树的任意节点最多只能有两个子节点
• 二叉树的子树仍然是二叉树
• 如果只有一个子节点，可以是左子树，也可以是右子树
• 既然子树有左右之分，那么二叉树是有序树
  

综上二叉树有 5 种基本形态，如下图所示：



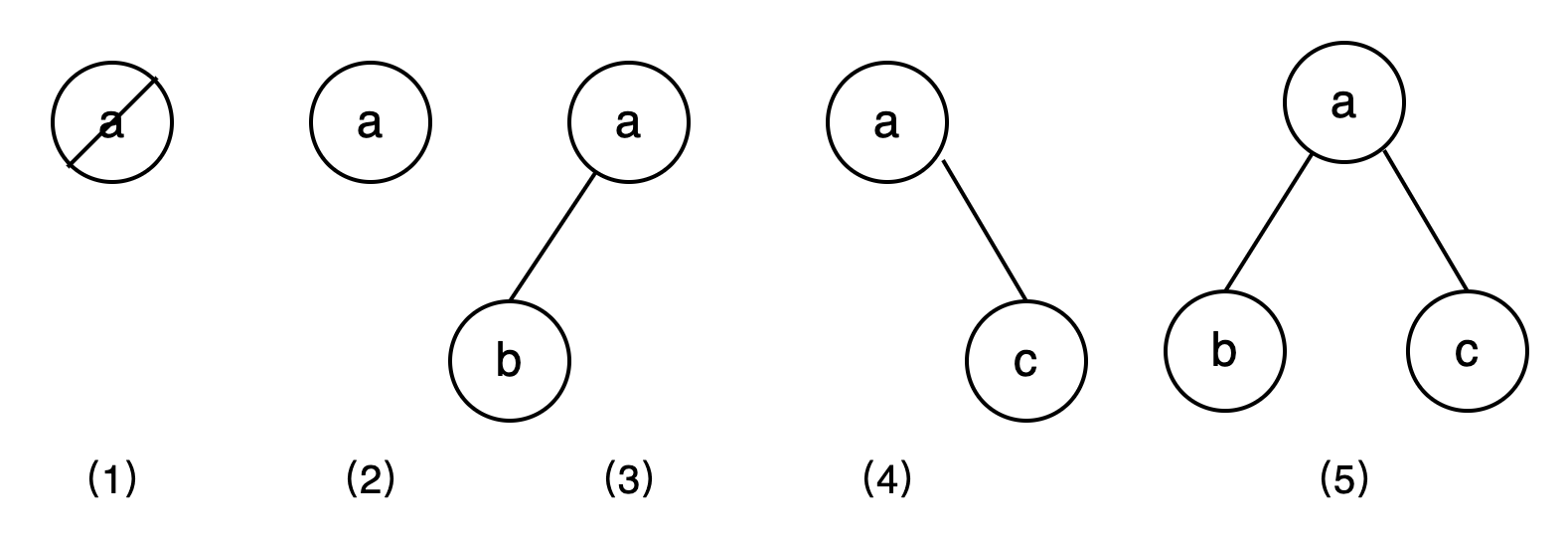
（1）为“空”，没有任何节点。

（2）仅有根节点，只有根节点，没有子节点。

（3）仅有左子树，只有一个子节点，且位于左子树位置，右子树位置为空。

（4）仅有右子树：只有一个子节点，且位于右子树位置，左子树位置为空。

（5）有左右子树：左右子树都有，这是最容易理解的二叉树结构。

通过（3）和（4）我们可知子树有左右之分，因此二叉树是有序树。

二叉树还可以进一步细分为两个特殊类型：满二叉树和完全二叉树。

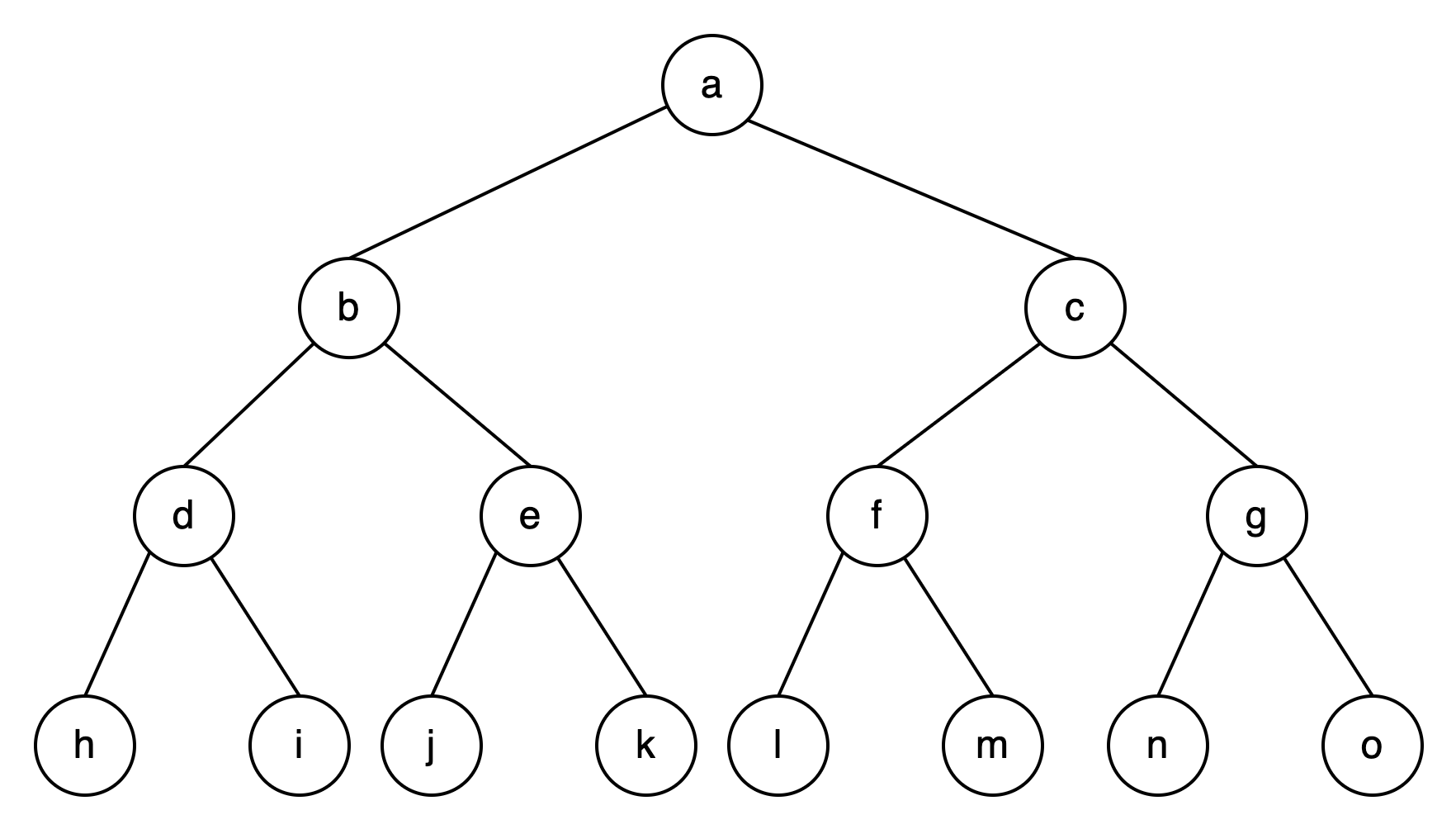
满二叉树：在二叉树中，除最下一层的叶节点外，每层的节点都有两个子节点，如下图所示：



完全二叉树：除二叉树最后一层外，其他各层的节点数都达到最大个数。

且最后一层从左向右的叶节点连续存在，只缺右侧若干节点，如下图所示：



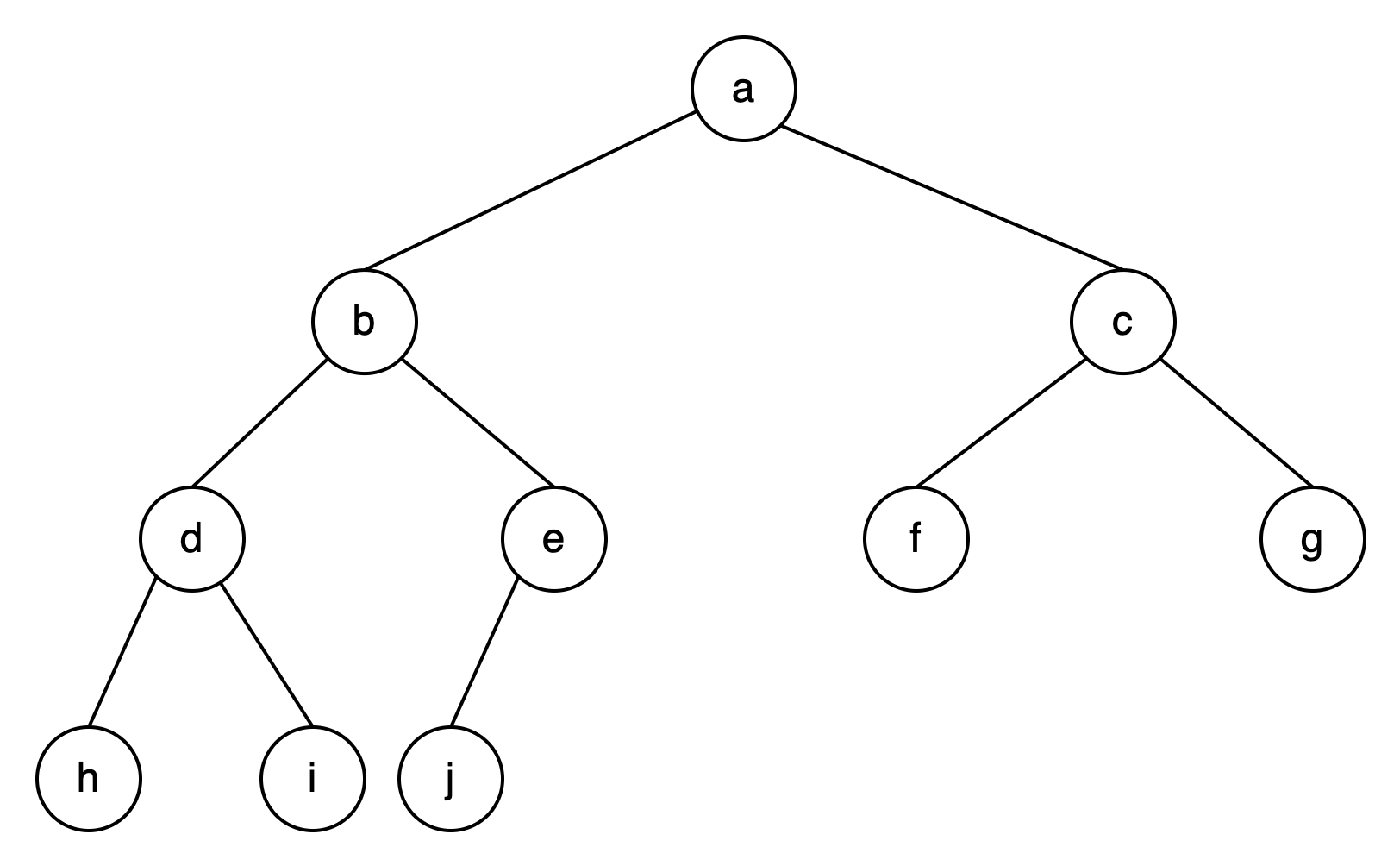
从上面对比图我们可以得出一个结论：

满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

• 根据二叉树的定义，还可以得出下面一些结论：
• 在非空二叉树中，第i层的节点总数最多为2^(i-1)（i≥1）个
• 深度为k的二叉树最多有2^k-1个节点（k≥1），最少有 k 个节点。
• 对于任意一棵二叉树，如果其叶节点数为 n₀，而度为 2 的节点总数为 n₂，则 n₀ = n₂ + 1
• 具有 n 个节点的完全二叉树的深度 k 为：k=[log2ⁿ]+1
• 有 n 个节点的完全二叉树各节点如果用顺序方式存储，对任意节点 i，有如下关系：
  
  • 如果 i！=1，则其父节点的编号为i/2；
  • 如果 2*i≤n，则其左子树根节点的编号为 2*i；若 2*i>n，则无左子树
  • 如果 2*i+1≤n，则其右子树根节点编号为 2*i+1；若 2*i+1>n，则无右子树
    
  
  

这些公式我们今天可能会用不到，到时给出来，帮助以后咱们更好的用二叉树进行算法设计。


堆是一个近似完全二叉树的结构，同时满足堆积的性质，即子结点的键值或索引总是小于（或者大于）它的父结点。

从这句话来看，堆必须满足以下两个条件：

• 是完全二叉树
• 子结点的键值或索引总是小于（或者大于）它的父结点
  

说下第二条：子结点的键值或索引总是小于（或者大于）它的父结点。

例如，有下面这样一棵完全二叉树：



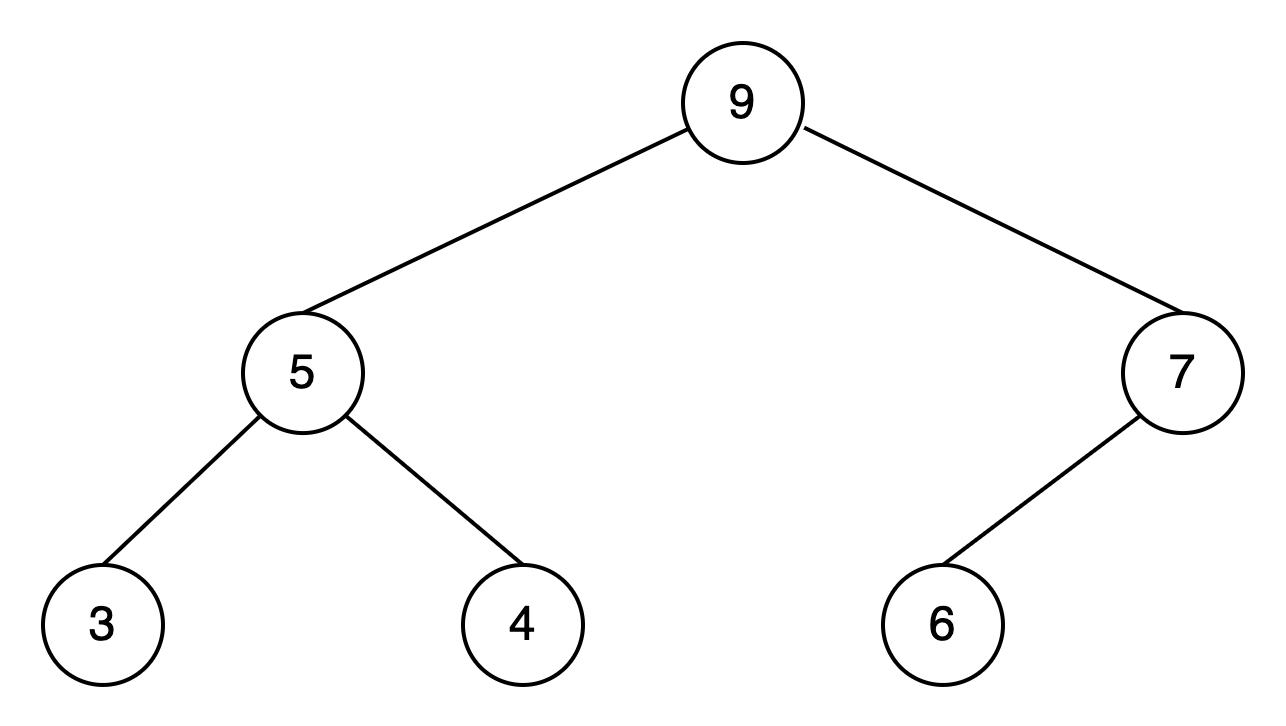
从图中可知，父结点 9 比子结点 5、7 大，父结点 5 比子结点 3、4 大，父结点 7 比子结点 6 大。

因此，它不但是一个完全二叉树，还满足子结点小于父结点的要求，这样的结构就称为堆。

堆结构中，我们是可以通过公式来确定某个结点的父结点和子结点的位置。

假设该结点的位置为 j，则其父结点位置为 (j-1)/2，小数则向下取整。

左子结点位置为 2*j+1，右子结点位置为 2*j+2。

我们为上图编号，来验证一下：



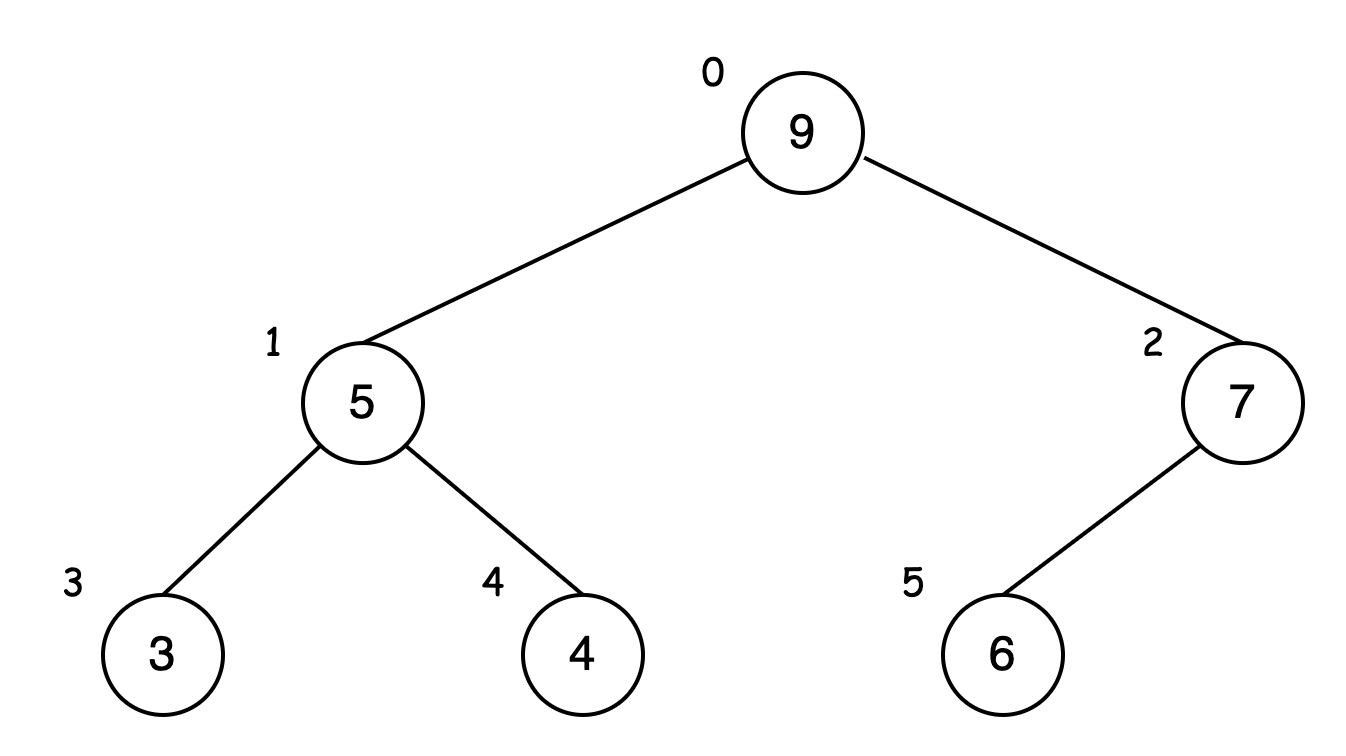
因为目前演示中只有父节点 9 和 节点 5 有左右两节点，我们就用结点 5，j=1 来测试公示。

则其父结点的位置计算如下：

父结点位置为 (1-1)/2=0， 位置 0 的数据是 9。

两个子结点的位置计算如下：

左子结点为 2*1+1=3，位置 3 的数据是 3。

右子结点为 2*1+2=4，位置 4 的数据是 4。

我们就可以基于堆的公式，来对数据进行排序。

既然是排序，堆排序也可以分为递增和递减两种排序。

递增：每个结点的值都大于或等于其子结点的值。

递减：每个结点的值都小于或等于其子结点的值。

假设有数据：99, 66, 88, 55, 3, 23，编写代码按照递增顺序进行堆排序。

我们首先按照从左到右顺序将数据放到二叉树中：



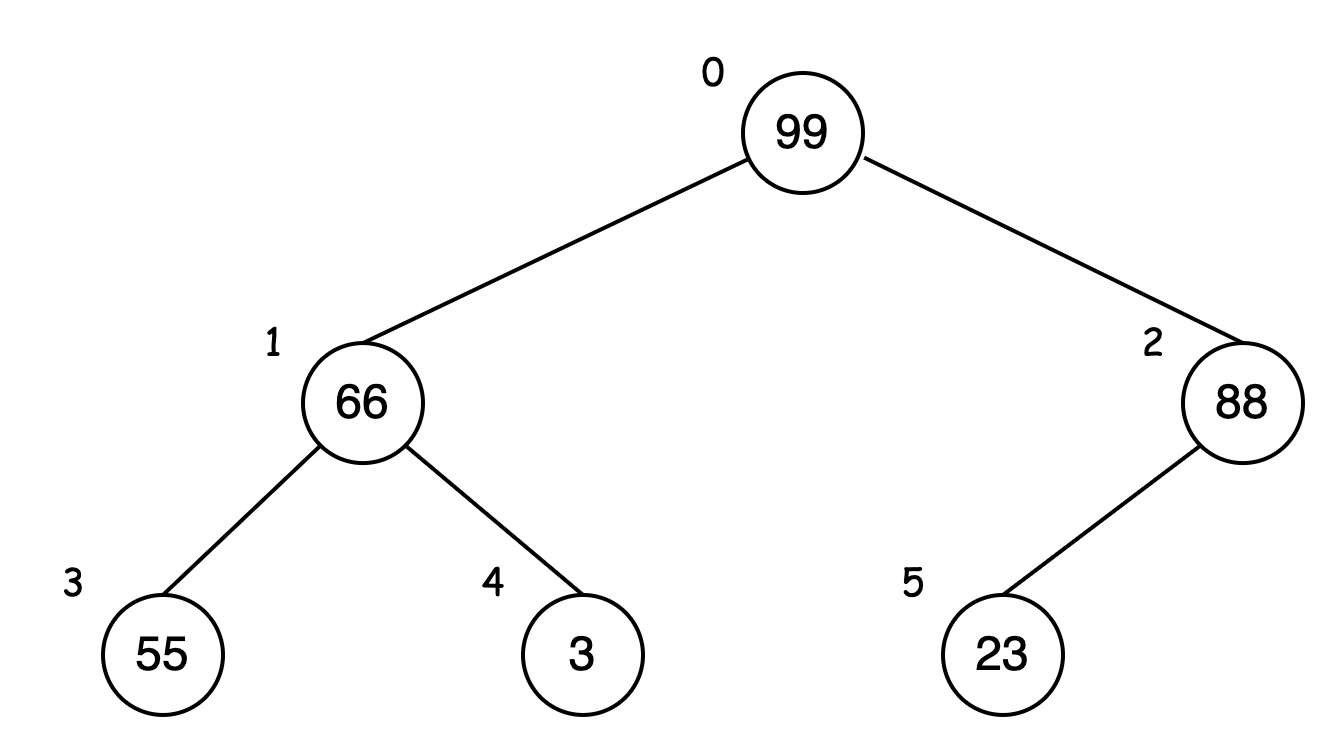
我们需要从小到大排序，按照堆的特性（父结点要大于子结点）交换数据，

从上图可知，每个父结点的数据都比其子结点大，因此，父结点 99 就是数据的最大值。

此时需要将此完全二叉树最底层且最右侧的数据与父结点进行交换，即数据 23 与 99 进行交换：



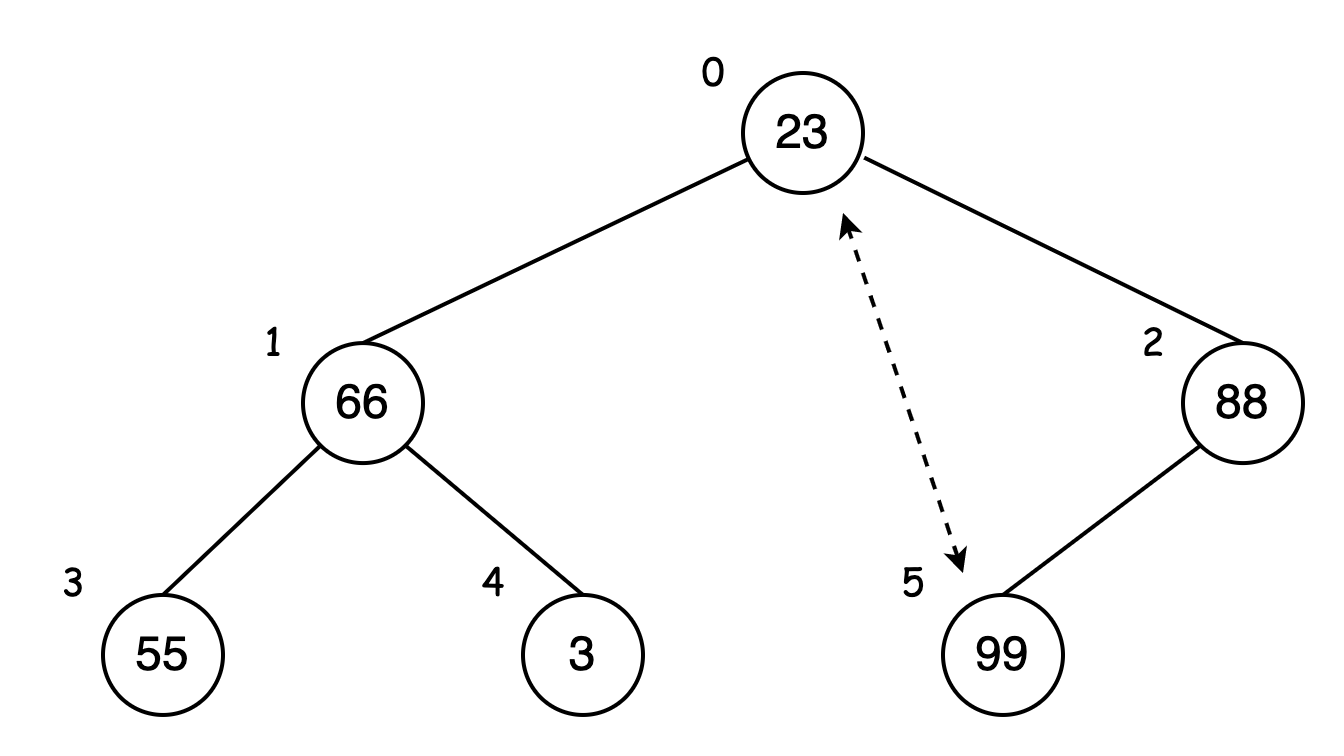
将数据 99 分支砍掉，放到排序后的数列里：



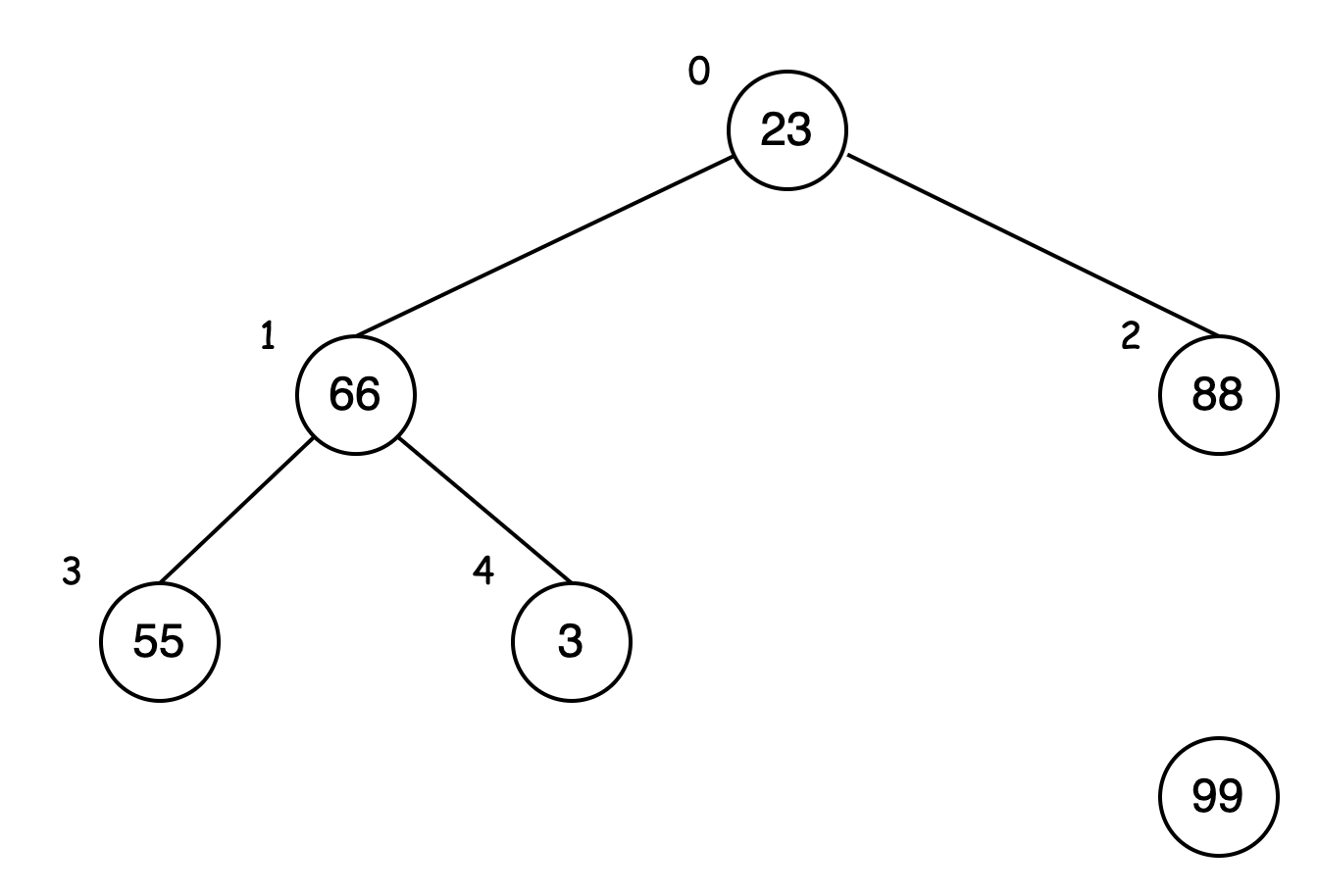
接下来用父结点 23 与其子结点 66、88 进行比较。

66 大于 23，两者交换位置：



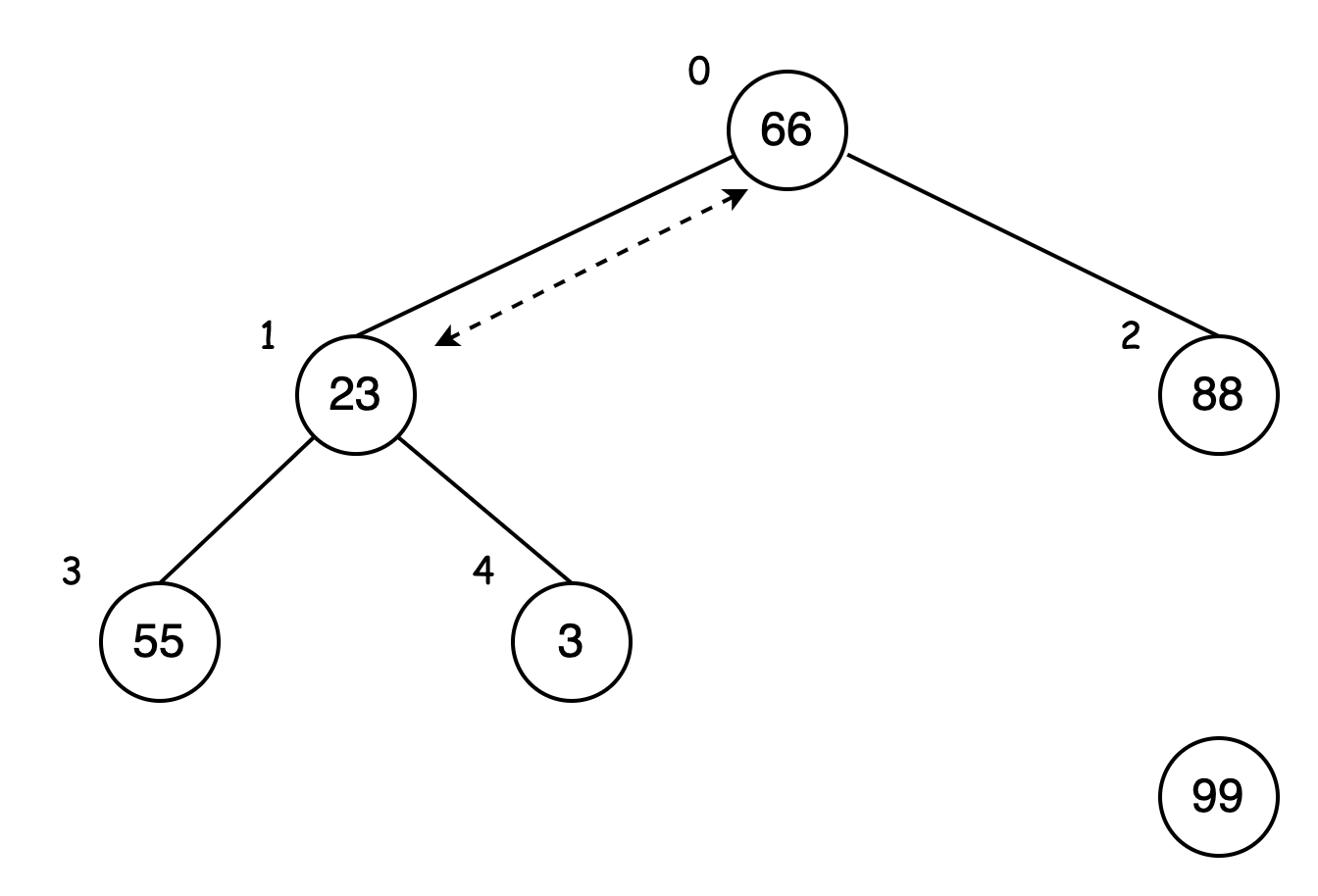
交换后再来看以数据 23 为父结点的分支，左子结点  55 比 23 大，交换位置：



此时 23 比 3 大，不需要交换位置。

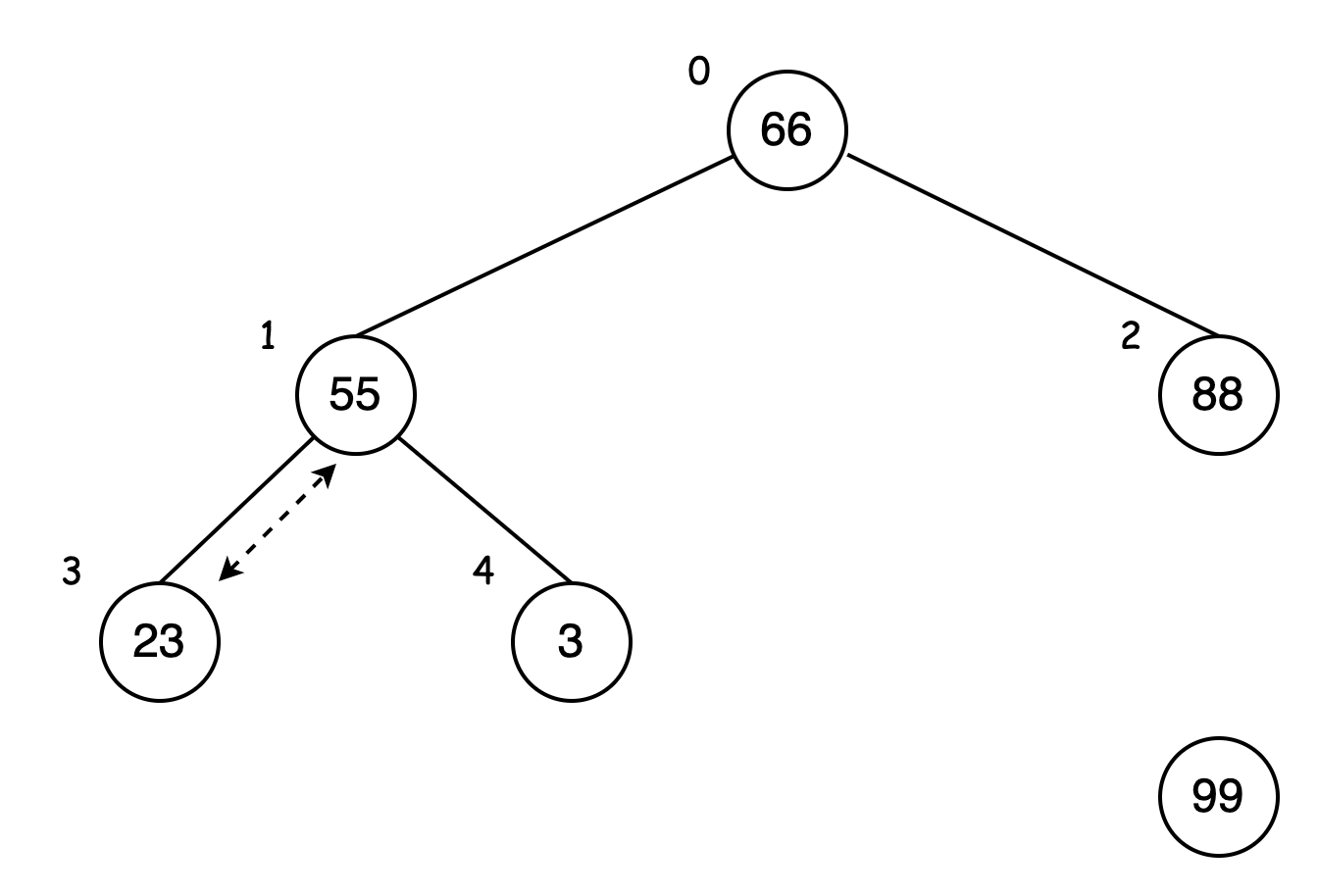
比较父结点 66 与其子结点 55、88。

88 比 66 大，交换 66与 88：



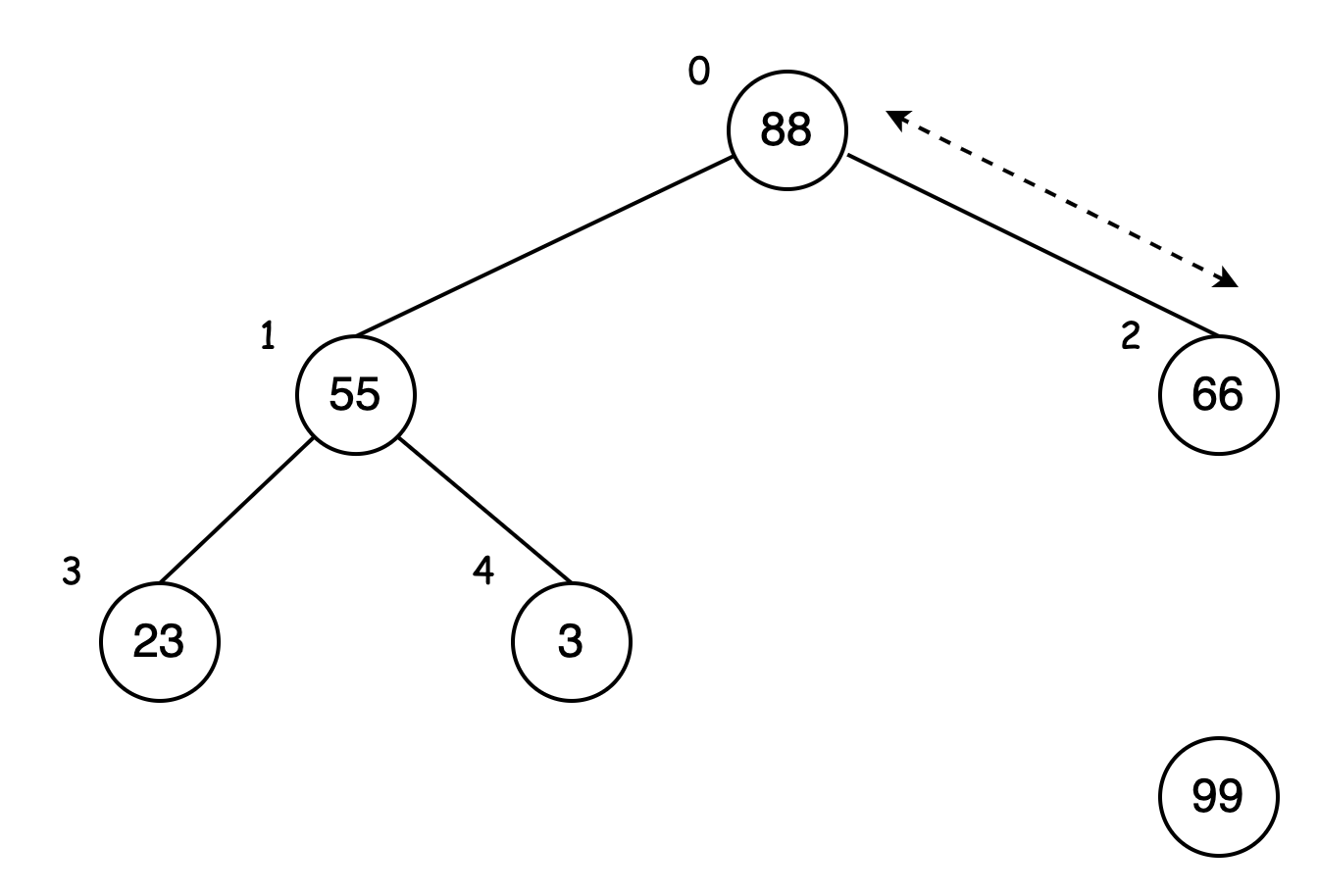
交换完之后，88 为父结点，是当前二叉树中最大的数字。

将 88 与此二叉树最底层最右侧的数据 3 进行交换：



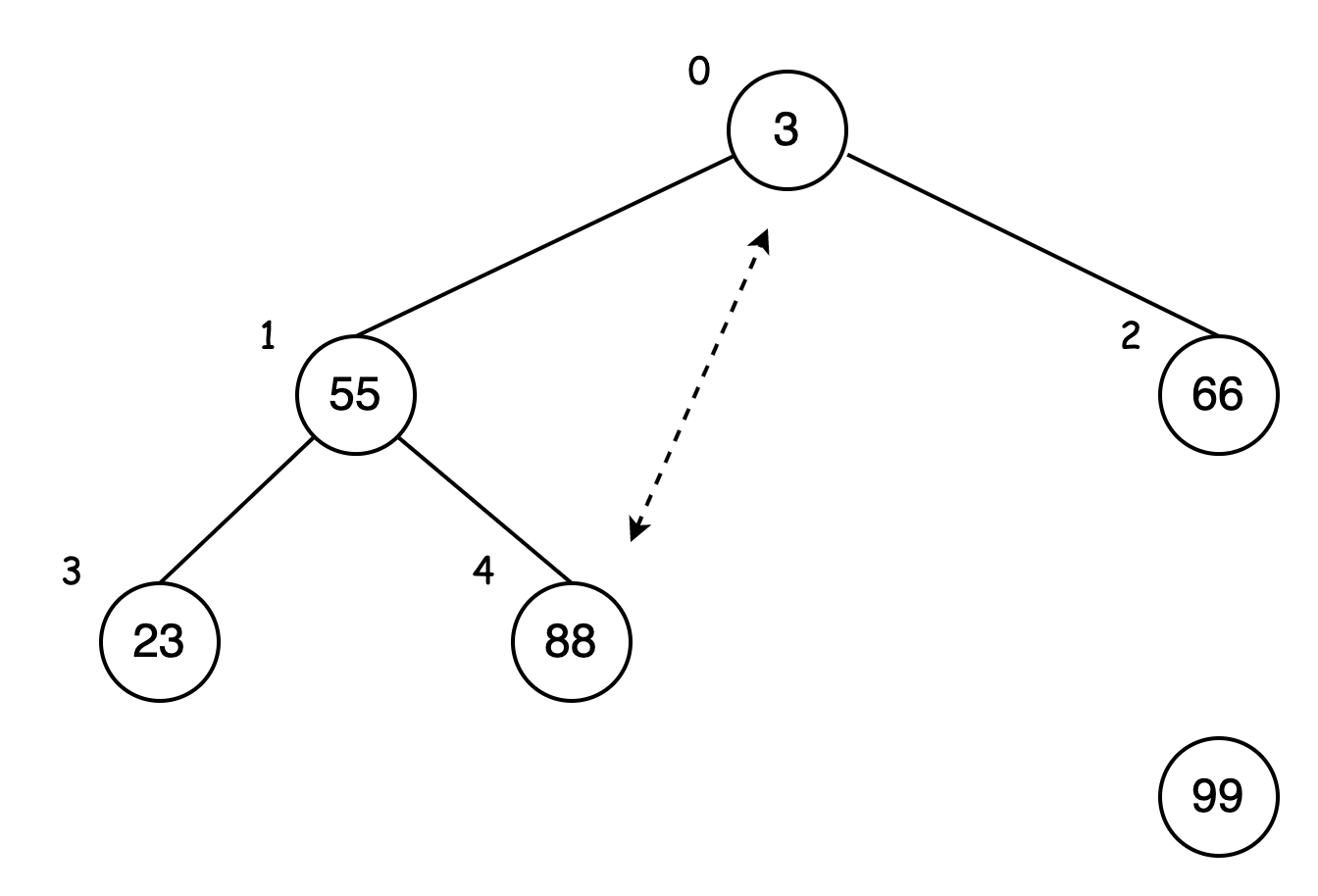
交换完之后，将 88 分支砍掉，放在 99 前：



此时数据 3 为父结点，将其与子结点 55、66 比较。

先比较左子结点，55 比 3 大，交换位置：



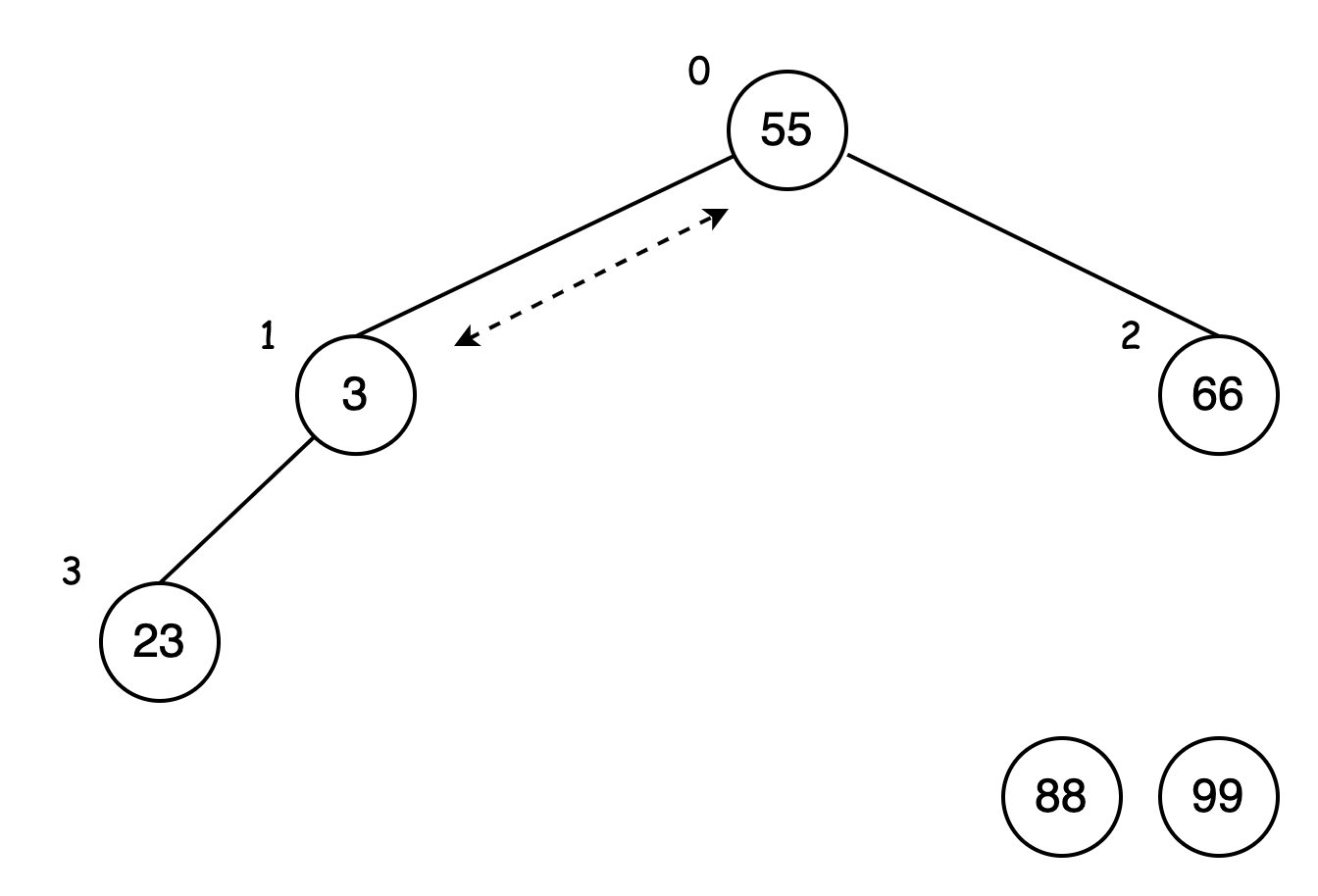
交换后再比较以 3 为父结点的分支，其子结点 23 大于 3，交换位置：



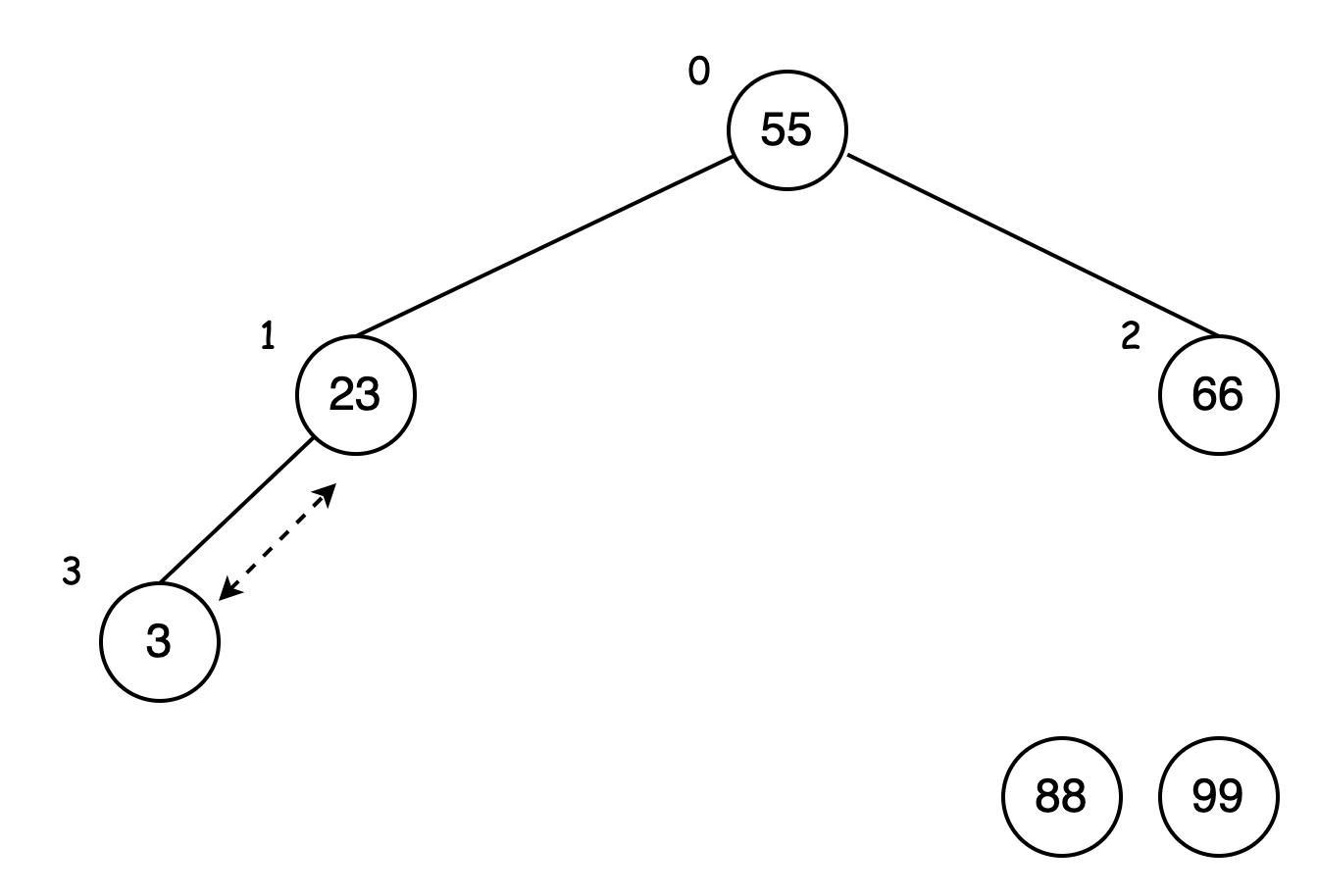
父节点 55 再与右结点 66 比较，66 大于 55，交换位置：



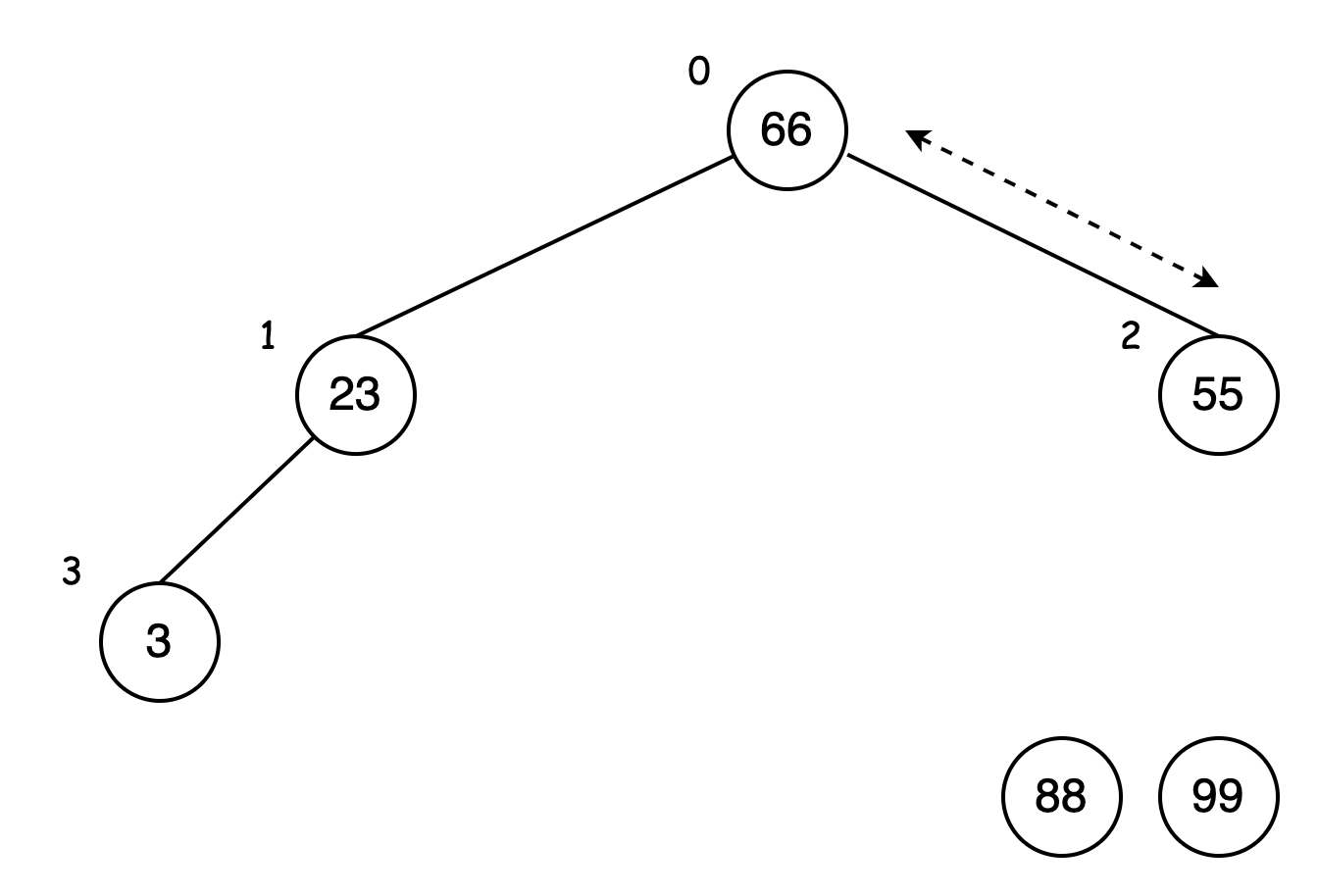
66 是当前二叉树的最大值，将数据 66 与完全二叉树最底层最右侧的数据 3 交换，并砍掉 66 分支，放到数据 88 前：



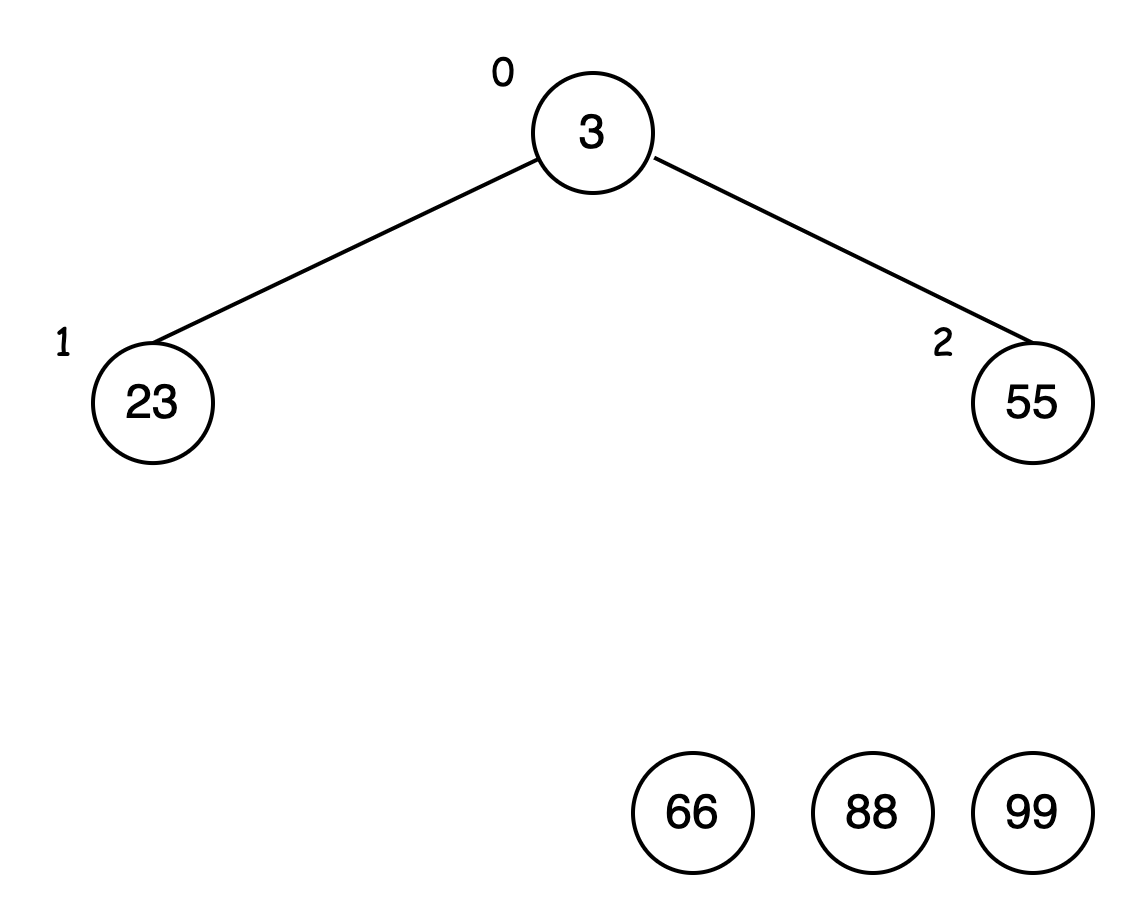
此时的二叉树以 3 为父结点，小于其子结点 23，交换位置：



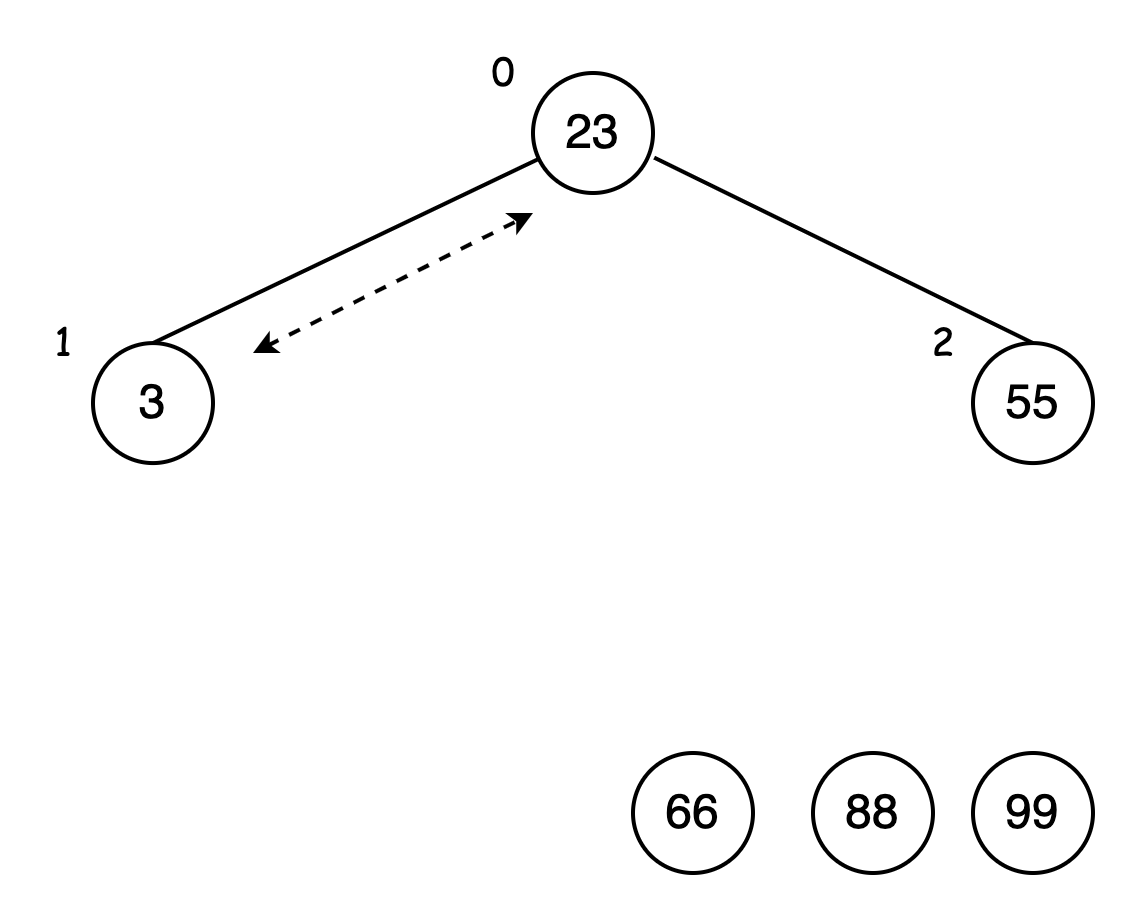
父节点 23 再与右节点 55 比较，55 大于 23，交换位置：



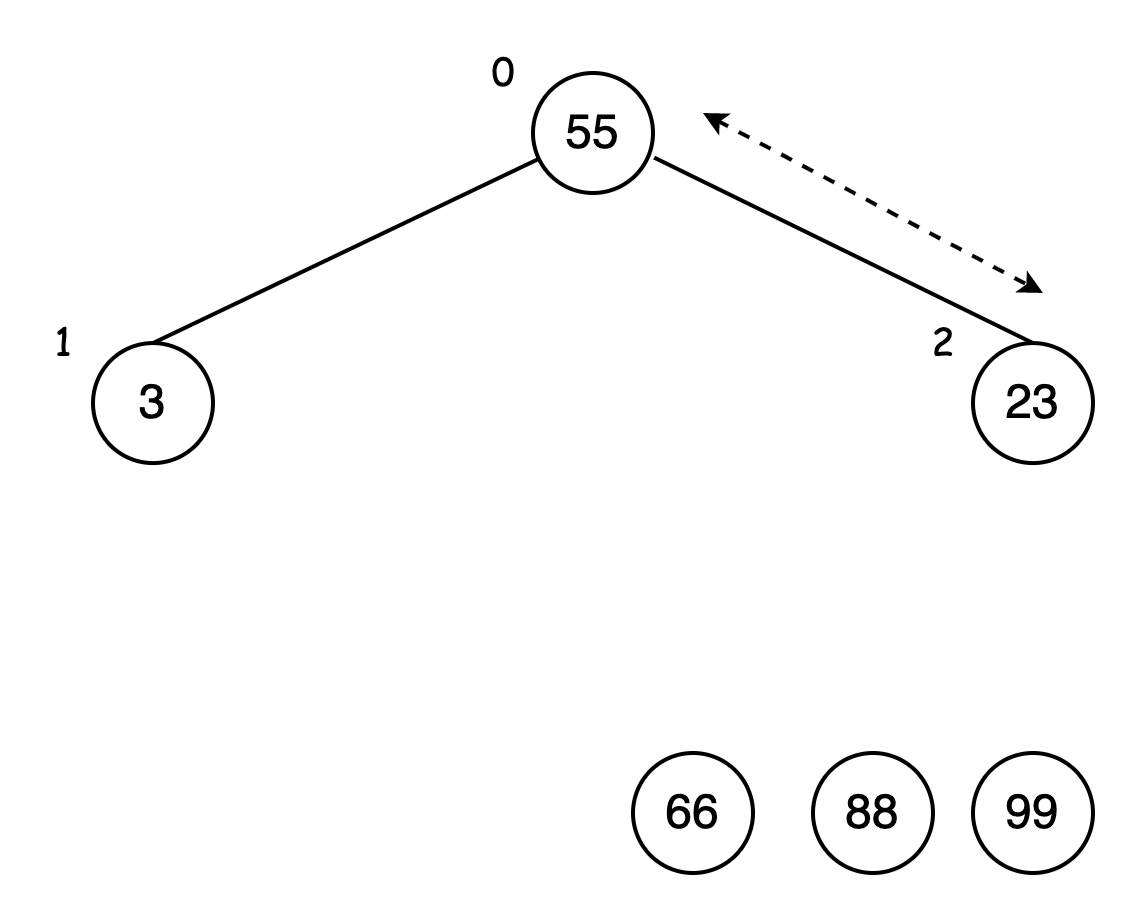
55 是当前二叉树的最大值，将数据 55 与完全二叉树最底层最右侧的数据 23 交换，并砍掉 55 分支，放到数据 66 前：



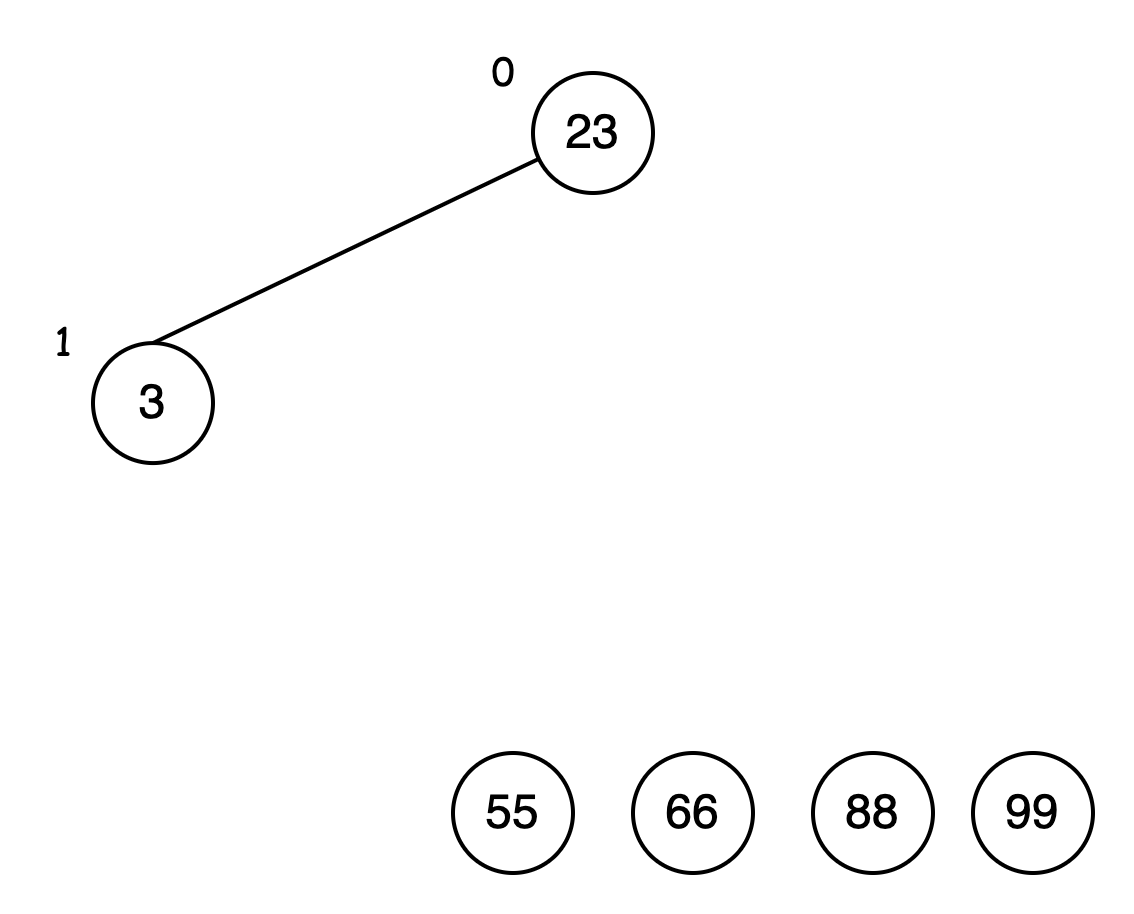
此时只剩数据 23和 3，该二叉树也满足堆。

因此直接将 23 放到数据 55 前，3 放到数据 23 之前，最后的排序结果：



从上面的步骤可知堆排序算法中，每次都需要用父结点和子结点进行比较，并交换。

接下来我们就要用 Python 编码实现上述过程啦。

初始化部分和之前一样，打印排序前和排序后的数据：

data = [99,66,88,55,3,23]
print("原始数据：")
for k in range(len(data)):
    print(f"{data[k]}",end=' ')
print('\n----我是分界线------\n')
print("堆排序后结果：")
heapSort(data)
for k in range(len(data)):
          print(f"{data[k]}",end=' ')     

接下来进入重点，实现 heapSort(data)。

heapSort(data) 就是用来定义堆排序函数。

我们首先要将根结点取出，与最后一位对调。对前面 len-1 个结点继续进行堆调整过程。

而上面这个过程，是一个独立操作，我们可以放到另一个函数来实现：

def heapSort(heap):
    buildHeap(heap)

在 buildHeap(heap) 中，将堆中所有数据重新排。

首先获取堆长度，然后自下向上构建堆。

这样在构建过程中，我们要调整列表中的元素，保证是以 i 为父结点的堆，并保证 i 是最大值：

def buildHeap(heap):
    heap_len = len(heap)
    for i in range((heap_len -2)//2,-1,-1):
        heapBasic(heap, heap_len, i)

heapBasic(heap, heap_len, i) 又是一个独立过程，需要判断每个节点的关系。

例如知道某个结点的下标 i，那么则其父结点、左子结点、右子结点的下标都可以计算出来。

在一开始就介绍过公式，这里就不解释了。

父结点：

(i-1)//2

左子结点：

2*i + 1

右子结点：

2*i + 2 

即左子结点 + 1。

虽然 heapBasic() 还没有实现，但是此时 buildHeap(heap) 就构建好了。

这样最开始 heapSort(heap) 中调整后列表的第一个元素就是最大的元素，与最后一个元素交换，然后将剩余列表递归调整为最大堆：

def heapSort(heap):
    buildHeap(heap)
    for i in range(len(heap)-1, -1, -1):
        heap[0], heap[i] = heap[i], heap[0]
        heapBasic(heap, i, 0)

现在就剩 heapBasic() 没有实现了，新建函数完成节点判断部分：

def heapBasic(heap,heaplen,i):
    left = 2*i + 1
    right = 2*i + 2

讲每次最大值赋给变量 larger：

    larger = i

如果左子结点位置小于堆长度，同时堆的最大值小于左子结点的值，将左结点位置给 larger：

    if left < heaplen and heap[larger] < heap[left]:
        larger = left

如果右子结点位置小于堆长度，同时堆的最大值小于右子结点的值，将右子结点位置给 larger：

    if right < heaplen and heap[larger] < heap[right]:
        larger = right

如果做了堆调整，则 larger 的值等于左子结点或右子结点的值。

再做堆调整操作，此时就可以通过递归实现：

    if larger != i:
        heap[larger], heap[i] = heap[i], heap[larger]
        heapBasic(heap, heaplen, larger)

运行看结果：



编码就是重复之前的操作，难点在于理解 heapBasic() 中这几个重要参数：

• heap: 表示堆
• heaplen: 表示堆的长度
• i: 表示父结点的位置
  

要想理解程序，一定要自己动手排序哦～

好了，下课！

源码：

游客，如果您要查看本帖隐藏内容请回复

yiyuqi

Nate_2020

malgave

王英杰W

hornwong

Hyjxsssss

done

Thunderbee

鱼C-小师妹

已更，学起来！

1molHF

学习

hornwong

鱼C-小师妹

怂小白

学习学习

奥古斯都丶

青出于蓝

学习

青出于蓝

学习

一点点儿

学习学习

cancry

学习学习

憨憨学py

zhangjinxuan

学习