一元三次方程求根公式

傻眼貓咪

这是最近研究，随便写的代码，再不发，就石沉大海了（电脑一堆几百个项目里面，很多精彩的代码都随便乱取名，然后忘记发，后面又懒得发了 我是猪吗？）

以一元二次方程 Quadratic equation 为前提，
通过化简后，只含有一个未知数（一元），并且未知数的最高次数是2（二次）的整式方程，叫做一元二次方程（quadratic equation with one unknown）。

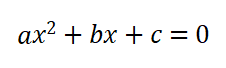
其求根的公式是：

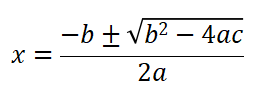
判别式是：

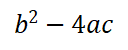
只会有三种情况；
判别式 = 0 两个根相同
判别式 < 0 无实数根
判别式 > 0 有两个不相同的根

一元三次方程 Cubic equation

但如果是一元三次方求根公式，相对较困难（目前已知能找出一元四次方程求根公式，而五次方程还没有人找到）

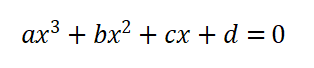
我的代码是运用盛金公式（因为我觉得相对比较容易理解）
盛金公式有两种判别式：
（一）重根判别式

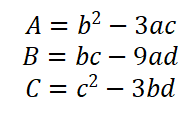
（二）总判别式


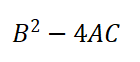
会有四种情况，对应不同求根公式；
（一）当 A = B 时，三个根相同


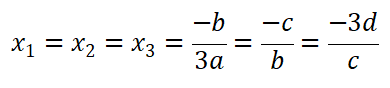
（二）当 总判别式 > 0 时，一个实数根和两个带有虚数根



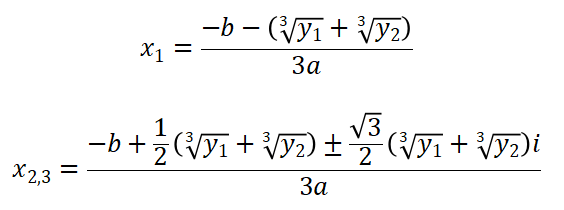
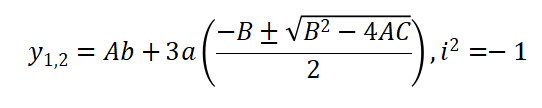
（三）当 总判别式 = 0 时，三个根，其中两个根相同



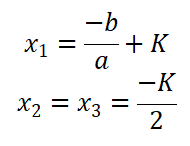
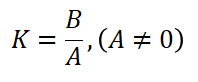
（四）当 总判别式 < 0 时，三个根都不相同



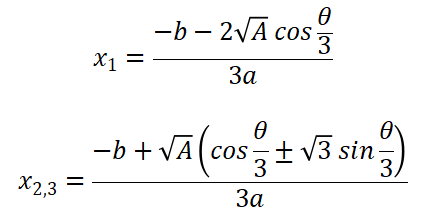
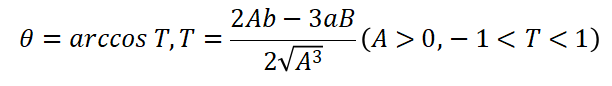
例子：x^3 + 5x^2 - 2x - 24 = 0
根是：-4、2、-3

我的代码：

#include <iostream>
#include <complex>
#include <cmath>

using std::complex, std::operator<<, std::ostream;
class Roots {
        friend ostream& operator<<(ostream&, const Roots&);
public:
        complex<int> x1, x2, x3;
        Roots();
        Roots(complex<int>, complex<int>, complex<int>);
};

ostream& operator<<(ostream& OS, const Roots& R)
{
        if (R.x1.imag() or R.x2.imag() or R.x3.imag()) {
                char a, b, c;
                a = R.x1.imag() < 0 ? '-' : '+';
                b = R.x2.imag() < 0 ? '-' : '+';
                c = R.x3.imag() < 0 ? '-' : '+';
                OS
                        << R.x1.real() << a << R.x1.imag() << "i, "
                        << R.x2.real() << b << R.x2.imag() << "i, "
                        << R.x3.real() << c << R.x3.imag() << "i"
                        << std::endl;
        }
        else {
                OS << R.x1.real() << " " << R.x2.real() << " " << R.x3.real() << std::endl;
        }
        return OS;
}
Roots::Roots() : x1(0), x2(0), x3(0) { }
Roots::Roots(complex<int> a, complex<int> b, complex<int> c) : x1(a), x2(b), x3(c) { }

// 一元三次方程式
class CubicEquation {
public:
        int a, b, c, d;
        Roots R;
        CubicEquation(int, int, int, int);
private:
        int A, B, C;
        double D;
};

CubicEquation::CubicEquation(int a, int b, int c, int d) : a(a), b(b), c(c), d(d) {
        A = b * b - 3 * a * c;
        B = b * c - 9 * a * d;
        C = c * c - 3 * b * d;
        D = B * B - 4 * A * C;
        if (A == B and !B) {
                R = { -b / 3 * a, -c / b, -3 * d / c };
        }
        else if (D > 0) {
                double y1, y2;
                y1 = A * b + 3 * a * ((-B + sqrt(B * B - 4 * A * C)) / 2);
                y2 = A * b + 3 * a * ((-B - sqrt(B * B - 4 * A * C)) / 2);
                complex<int> x1{ static_cast<int> (round((-b - (pow(y1, (1. / 3)) + pow(y2, (1. / 3)))) / (3 * a))) };
                complex<int> x2{ static_cast<int> (round((-b + .5 * (pow(y1, (1. / 3)) + pow(y2, (1. / 3)))) / (3 * a))), static_cast<int> (round(((sqrt(3) / 2) * (pow(y1, (1. / 3)) + pow(y2, (1. / 3)))) / (3 * a))) };
                complex<int> x3{ static_cast<int> (round((-b + .5 * (pow(y1, (1. / 3)) + pow(y2, (1. / 3)))) / (3 * a))), static_cast<int> (round(-((sqrt(3) / 2) * (pow(y1, (1. / 3)) + pow(y2, (1. / 3)))) / (3 * a))) };
                R = { x1, x2, x3 };
        }
        else if (not D) {
                int K = B / A,
                        x1 = -b / a + K,
                        x2, x3 = x2 = -K / 2;
                R = { x1, x2, x3 };
        }
        else {
                auto T = (2 * A * b - 3 * a * B) / (2 * sqrt(A * A * A));
                int x1 = static_cast<int> (round((-b - 2 * sqrt(A) * cos(acos(T) / 3)) / (3 * a))),
                        x2 = static_cast<int> (round((-b + sqrt(A) * (cos(acos(T) / 3) + sqrt(3) * sin(acos(T) / 3))) / (3 * a))),
                        x3 = static_cast<int> (round((-b + sqrt(A) * (cos(acos(T) / 3) - sqrt(3) * sin(acos(T) / 3))) / (3 * a)));
                R = { x1, x2, x3 };
        }
}

using std::cout, std::endl;
int main(void) {
        // x^3 + 5x^2 - 2x - 24 = 0
        CubicEquation E(1, 5, -2, -24);
        cout << E.R;
        return 0;
}

-4 2 -3

柿子饼同学

大佬大佬 ORZ

努力的小鲤鱼

好优秀

森亦简

好长，码着，等学了C再看

Roy_wang

大佬厉害，学习学习

corgi

好厉害，先保存着

nusiew

鼓励！

香蕉那个不拿拿

大佬厉害，学习学习

sfqxx

3次方程还可以2分求解