|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
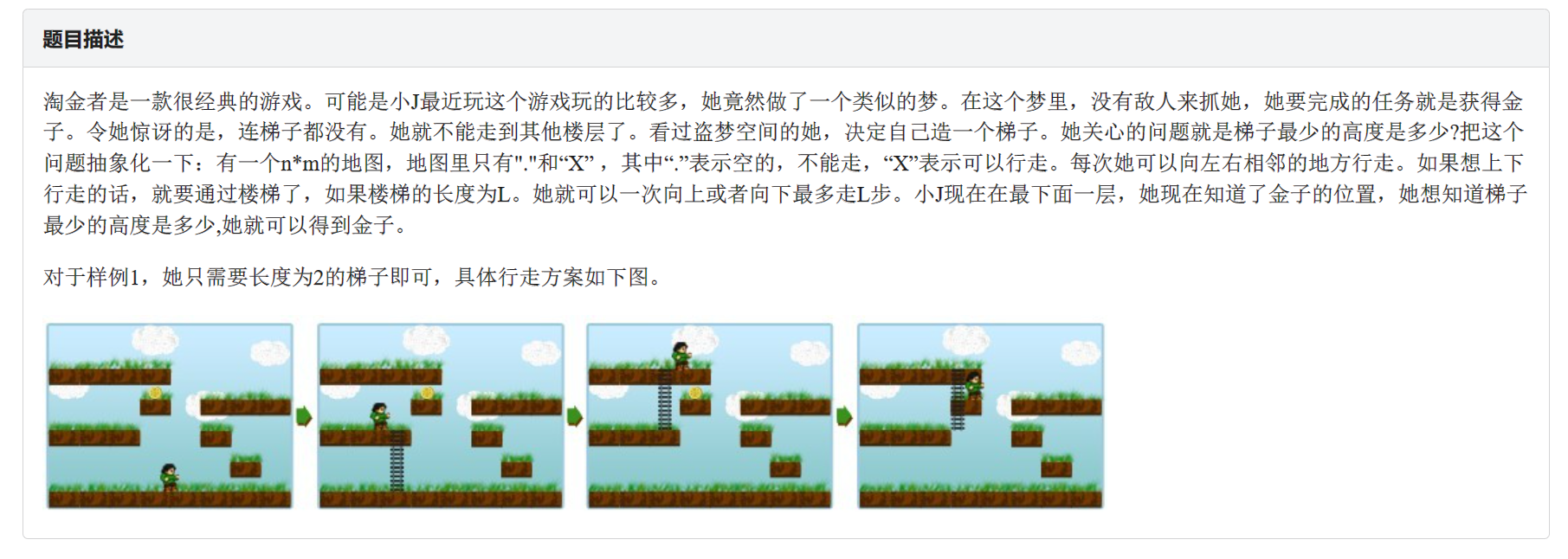
题解是深搜 + 二分梯子长度 , 但是深搜的代码不理解 , 求解释
输入输出:- 5 8
- XXXX....
- ...X.XXX
- XXX..X..
- ......X.
- XXXXXXXX
- 1 3
题解 :- #include <bits/stdc++.h>
- using namespace std;
- int n, m, x, y, mid, vis[205][205], i, j, k, l, r, ans, o, p;
- char S[205][205];
- void dfs(int x, int y) { // 深搜代码不理解 , 跟梯子长度有什么关系
- if (vis[x][y] || S[x][y] == '.')
- return;
- vis[x][y] = 1;
- if (y > 1)
- dfs(x, y - 1);
- if (y < m)
- dfs(x, y + 1);
- for (int i = 1; i <= mid; i++) {
- if (x > i)
- dfs(x - i, y);
- if (x + i <= n)
- dfs(x + i, y);
- }
- }
- int main() {
- cin >> n >> m;
- for (i = 1; i <= n; i++) cin >> S[i] + 1;
- cin >> x >> y;
- r = 205;
- while (l <= r) {
- mid = (l + r) >> 1;
- memset(vis, 0, sizeof(vis));
- dfs(n, m);
- if (vis[x + 1][y + 1])
- ans = mid, r = mid - 1;
- else
- l = mid + 1;
- }
- cout << ans;
- return 0;
- }
首先要搞明白“二分查找答案”是一个什么样的模式:当问题要求满足某个条件的最大/最小值时,如果任何一个给定的值是否满足条件是非常容易判定的,同时值大小到是否满足条件的映射是单调的,也就是说任何一个值如果满足条件,那么任何比该值更大/更小的值一定也满足条件,这时就通常可以尝试考虑二分答案。二分答案就是利用单调性,二分查找答案的值,每次判定当前范围的中点是否满足条件,根据结果和单调性调整下一次迭代中的搜索范围。
那显然,为了判定当前的 mid 是否足够大,需要在 dfs 也就是判定过程中使用当前 mid 的值,这一值决定了此次 dfs 中一次最多能向上/下移动的距离。
(说实话这个代码已经看懂二分梯子长度还没看懂我是没看懂的……感觉最难看懂的实际上是 cin >> S[i] + 1 这句话)
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)