马上注册，结交更多好友，享用更多功能^_^
您需要 登录 才可以下载或查看，没有账号？立即注册
x
本帖最后由 柿子饼同学 于 2022-8-26 17:26 编辑
ST 表 (C++版)
ST 表 的应用
ST 表 用于静态查找区间最值.
在一个数组中 , 给定一段区间 [L, R] 问你这段区间里的 最大值 / 最小值 是啥.
普通的方法我们当然可以从 L 到 R 遍历一遍 , 但是 , 当元素特别多 , L, R 太大 , 询问次数很多时 , 就会非常的慢 
这让我们想到了预处理, 这样不管问什么 , 我们都可以很快回答出来 !
于是 , 就有了 ST表 这么一个东西
原理
首先我们有一个数组 arr[ ] 来装值
我们定义一个二维数组 dp[ ][ ] (是的 , ST 表其实是一种动态规划的思想)
dp[j] 表示 arr 的第 i 个元素和它后面 2 ^ j 个元素中的最大值 , 区间是 [i, i + 2^j-1]
为什么这样定义呢 ?
因为每个整数都可以表示成 2^x + 2^y + ... 这样的形式
我们可以通过拼接的方式把目标区间用它 "拼" 成一个完整区间
例如 , 区间 [10, 24] 的最大值可以用 dp[10][3], dp[18][2] 和 dp[22][1] 的最大值 来表示
( dp[10][3] -> [10, 10 + 2^3] -> [10, 18] , 以此类推 )
但是这样有点麻烦 , 有没有更快的方法呢 ? 
当然有 ! 
我们可以直接把它的最大值表示为 dp[10][3] 和 dp[24 - 2^3][3] 的最大值
看图 :
图 1
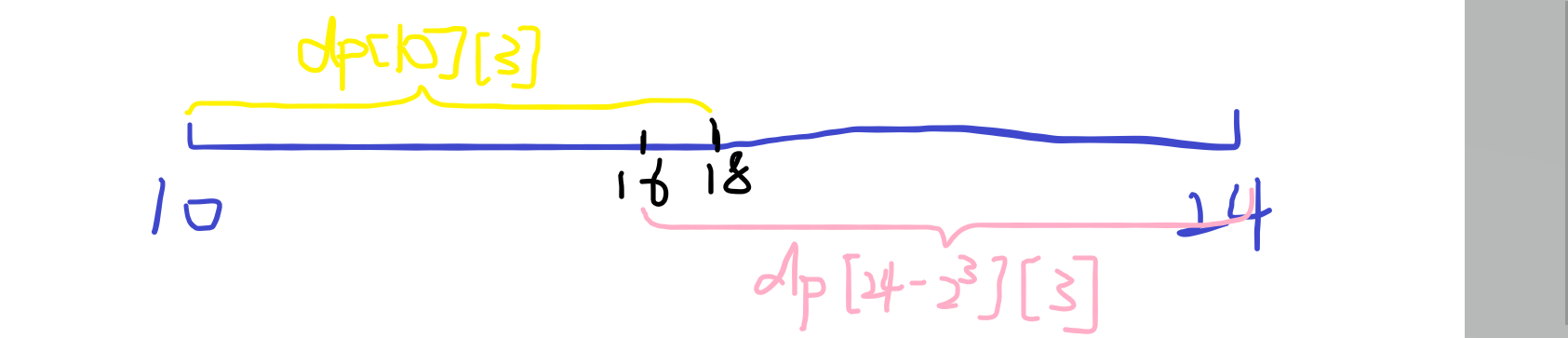
由于是取最值 , 所以重叠也没关系 , 只要到整个区间就行了
那我们怎么确定两个小区间的长度呢 ?
就是看大区间最大能 "装下" 2 的几次方 , 假设大区间长度是 l , 则一个小区间长度就是 log2 ( l ) 向下取整
由于 log 函数比较浪费时间 , 所以我们选择预处理 , 反正精度不高 , 我们有如下的递推式 : ( 这个就是个小公式 , 记住就行了 ) log_2 = log_2[i >> 1] + 1;
" >> " 是左移符号 , 可以理解为除以 2 的多少次方 , i >> 1 就是 i / 2 的意思
1 << x 就是 2 ^ x 的意思
然后我们就可以读入数据了 , 我们其实不需要单独的数组来存值 , 还记得 dp 的定义吗?
我们把 dp[0] 存入值就好了 , 因为 2 ^ 0 == 1, 区间长为1, 最大值就是它本身
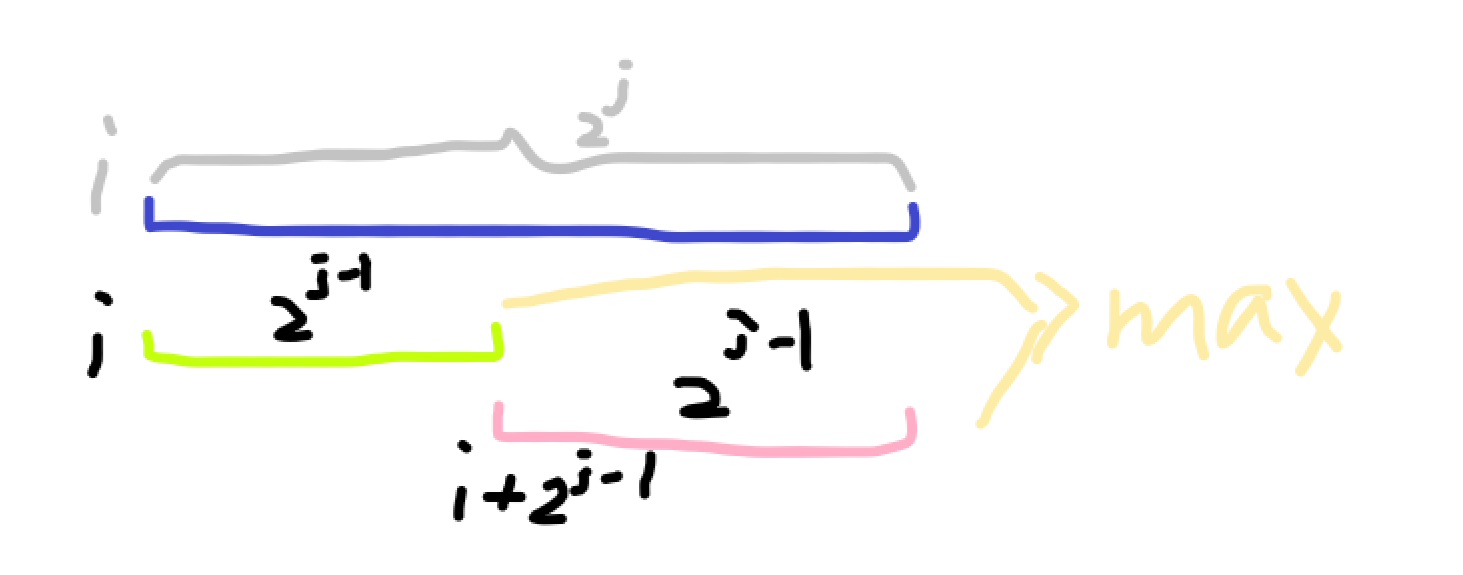
然后 , 就到了 dp 数组的预处理部分 :
由于 dp 第二维是表示 2的次方 , 所以每次增加就会乘 2 , 这个要注意
代码如下 : for(int j = 1; j <= log_2[n]; j++){ // 第一层枚举 j, 小区间长度
for(int i = 1; i + (1<<j) - 1 <= n; i++){ // 第二层枚举开始的下标, 注意不要越界
dp[j] = max(dp[j-1], dp[i+(1<<(j-1))][j-1]);
}
}
图 2
[/i]
原理可以看上图 , 一个大的区间最值等于它分成的两个小区间的最值
以上我们可以写一个初始化函数 : void init(){
for(int i = 3; i <= n; i++) log_2 = log_2[i >> 1] + 1;
for(int j = 1; j <= log_2[n]; j++){
for(int i = 1; i + (1 << j) - 1 <= n; i++){
dp[j] = max(dp[j-1], dp[i+(1 << (j-1))][j-1]);
}
}
}
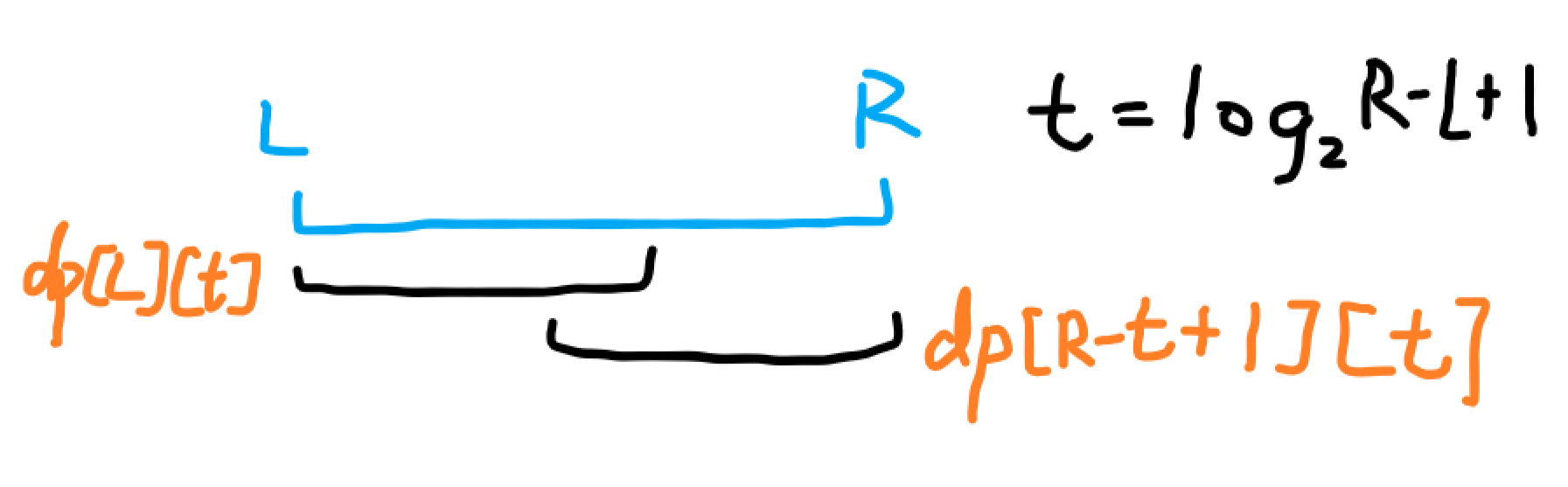
然后就是我们处理询问的区间 [L, R]
我们先求出 L 到 R 有多少个元素 , 一共是 R-L+1 个
[i] 还记得我们的重叠取法吗?[/i]
[i]
图 3
[/i]
根据以上内容我们可以写出代码了吧 :
int query(int l, int r){
int t = log_2[r-l+1];
return max(dp[l][t], dp[r-(1<<t)+1][t]);
}
好啦, 贴上完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int dp[N][24];
int log_2[N];
int n, q;
void init(){
for(int i = 2; i <= n; i++){
log_2 = log_2[i >> 1] + 1;
}
for(int j = 1; j <= log_2[n]; j++){
for(int i = 1; i + (1<<j) - 1 <= n; i++){
dp[j] = max(dp[j-1], dp[i + (1 << (j-1))][j-1]);
}
}
}
int query(int l, int r){
int t = log_2[r-l+1];
return max(dp[l][t], dp[r-(1<<t)+1][t]);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0); // 读入优化
cin >> n >> q;
for(int i = 1; i <= n; i++) cin >> dp[0];
init();
int l, r;
while(q--){
cin >> l >> r;
cout << query(l, r) << endl;
}
return 0;
}
[i][i][i]
[i]  ~感谢观看~ [/i]
[/i][/i][/i]
[i]
[/i]
[/i] |
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2022-8-26 16:32:14
置顶卡
千斤顶
显身卡
楼主
发表于 2022-8-26 17:16:51
发表于 2022-8-26 17:30:26
