其实你可以这样去想,用动态规划来思考
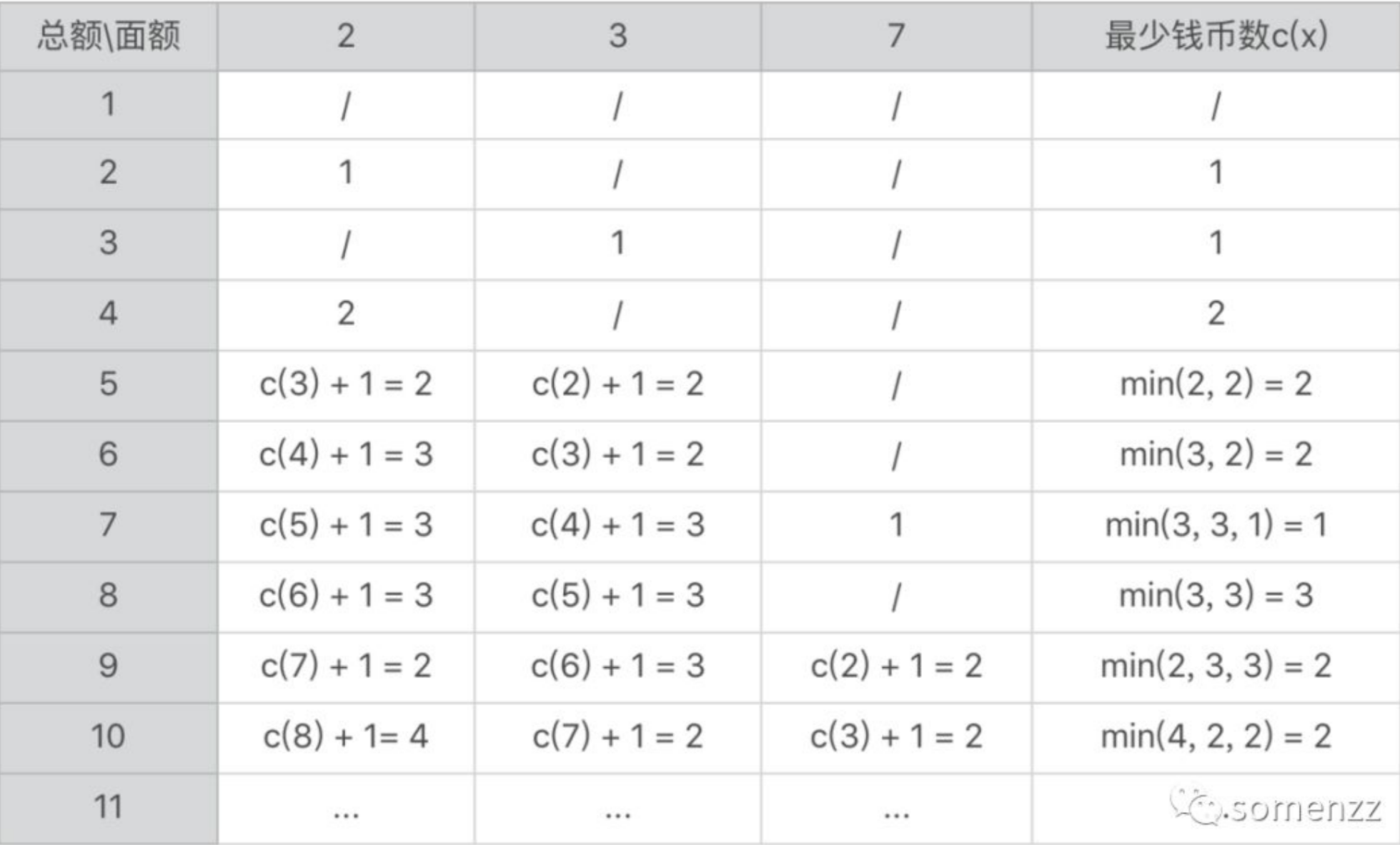
[b]什么是动态规划?[/b]在递归的时候,我们可以通过不断地分解问题,将复杂的任务简化为最基本的小问题,比如基于递归实现的归并排序,排列,组合等。不过有时候,我们并不用处理所有可能的情况,只要找到满足条件的最优解就可以了,这种情况下,我们需要在各种可能的局部解中,找出那些可能达到最优的局部解,而放弃其他的局部解,这个寻找最优解的过程叫动态规划。 [b]怎么判断一个问题是否可以由动态规划来解决?[/b]首先,如果一个问题有多种可能,看上去需要排列或者组合的思想,但是最终求的只是最优解,如最大值,最小值,最短子串,最长子串等,可以试试使用动态规划。 其实,状态转移方程是个关键。你可以用状态转移表来帮助自己理解整个过程。如果能找到准确的转移方程,那么离最终的代码实现也就不远了 。 这里说下什么是状态转移方程:从上一个状态到下一个状态之间可能存在一些变化,以及基于这些变化的最终决策结果。我们把这样的表达式称为状态转移方程。所有的动态规划算法中,状态转移是关键。 [b]来个例子[/b]假如有 2 块,3 块,7 块面额的纸币,如何使用最小的纸币数量来凑成 100 块。 一般会优先想到这样的方法:优先使用大面额的,不够的话再用次大面额的,直到凑成 100 块。100 除以 7 = 14 余数为 2 ,正好再用一张 2 的面额就可以了,也就是说最低 15 张。这属于贪心算法,今天先不讲。 动态规划的解题思路:c(n) 表示凑成 n 元的最小纸币数量c(100) = c(93 +7) = c(93)+1c(100) = c(97 +3) = c(97)+1c(100) = c(98 + 2) = c(98)+1 如果分析到这里,你可能会想到递归是一种解决思路,没错,但递归从大到小的分解其实保留了每一步的结果,并没有舍弃非最优解,效率并不高。 接下来就是找 c(93),c(97), c(98)哪个值最小,按照同样的方法,继续进行分解,直到 c(2) = 1,c(3) =1, c(4) = 2, c(5) = 2, c(6)=2, c(7)=1, c(8) = 3。这里可以推出状态转移方程:
状态转移方程

其中,c[i] 表示总额为 i 的时候,所需要的最少钱币数,其中 j=1,2,3,…,n,表示 n 种面额的钱币,value[j] 表示第 j 种钱币的面额。c[i - values(j)] 表示选择第 j 种钱币的时候,上一步为止最少的钱币数。需要注意的是,i - value(j) 需要大于等于 0,而且 c[0] = 0。
然后,从小到大,我们可以先在草纸上演算下,并验证状态转移方程
验证
接下来的事情就是将这种有规律的过程转化为源代码了,到这里其实已经没有难度了。 - #encoding = utf-8
- def count_dp(num):
- kinds = [2,3,7]
- ##循环使用tmp,降低内存占用
- tmp = [1,1,2,2,2,1,3]
- result = [[2],[3],[2,2],[2,3],[3,3],[7],[2,3,3]]
- if num <2:
- return
- elif 2 <= num <=8:
- return tmp[num-2],result[num-2]
- else:
- for i in range(9,num+1):
- values=[] #保留三个数据,取最小的那个
- for kind in kinds:
- values.append( (tmp[(i-2-kind)%7] + 1, (i-2-kind)%7 , kind) )
- min_value = min(values) ##默认按第一个值比较,取最小的
- #print(min_value)
- tmp_result = result[min_value[1]].copy()
- #print(tmp_result)
- tmp_result.append(min_value[2])
- #print(tmp_result)
- ##循环保存在临时数组中
- tmp[(i-2)%7] = min_value[0]
- result[(i-2)%7].clear()
- result[(i-2)%7] = tmp_result.copy()
- return tmp[(num-2)%7],result[(num-2)%7]
- def count_recursion(num):
- kinds = [2,3,7]
- ##循环使用tmp,降低内存占用
- tmp = [1,1,2,2,2,1,3]
- if num <2:
- return
- elif 2 <= num <=8:
- return tmp[num-2]
- else:
- ##采用递归方式
- values=[] #保留三个数据,取最小的那个
- for kind in kinds:
- values.append(count_recursion(num - kind))
- min_value = min(values)+1 ##默认按第一个值比较,取最小的
- return min_value
- if __name__ == "__main__":
- for i in [1,2,3,4,5,6,7,8,9,10,100]:
- print(i,'->',count_dp(i))
- for i in [1,2,3,4,5,6,7,8,9,15,20]:
- print(i,'->',count_recursion(i))
由于递归的方式特别慢,所以只让它运行到 20 。运行结果如下: - 1 -> None
- 2 -> (1, [2])
- 3 -> (1, [3])
- 4 -> (2, [2, 2])
- 5 -> (2, [2, 3])
- 6 -> (2, [3, 3])
- 7 -> (1, [7])
- 8 -> (3, [2, 3, 3])
- 9 -> (2, [2, 7])
- 10 -> (2, [3, 7])
- 100 -> (15, [2, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7])
- 1 -> None
- 2 -> 1
- 3 -> 1
- 4 -> 2
- 5 -> 2
- 6 -> 2
- 7 -> 1
- 8 -> 3
- 9 -> 2
- 15 -> 4
- 20 -> 4
注:本文转载自 https://cloud.tencent.com/developer/article/1758788 主题:动态规划-如何推导出状态转移方程
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)