|
|
马上注册，结交更多好友，享用更多功能^_^
您需要 登录 才可以下载或查看，没有账号？立即注册
x
本帖最后由 zhangjinxuan 于 2023-12-20 10:53 编辑
【FCOI #11】（FBC #1） 题解
官方题解：https://fishc.com.cn/forum.php?m ... d=237189&page=1
比赛链接：https://www.luogu.com.cn/contest/143425
这一篇云剪贴板是 FCOI #11(FBC #1) 所有题目的题解，供大家学习参考。
A 互关
提取关键信息，进行梳理，得出一个人想要与 sfqxx1 互关的条件如下：
1. e > a
2. [b ] = 1
3. f > c
4. [d] = 0 or [g]=1
根据以上梳理内容，可以轻松写出代码：
#include <bits/stdc++.h>
using namespace std;
int t;
long long e, f, a, c;
string g, b, d;
int main() {
scanf("%d", &t);
cin >> e >> f >> g;
while (t--) {
cin >> a >> b >> c >> d;
if (e >= a && f >= c && b == "YES" && (g == "YES" || d == "NO")) {
cout << "YES" << endl;
} else cout << "NO" << endl;
}
return 0;
}
B1 高斯记号
可以使用小数进行模拟：
#include <bits/stdc++.h>
using namespace std;
int main() {
int p;
double x;
scanf("%d%lf", &p, &x);
if (p - 1) cout << x - floor(x);
else printf("%d\n", (int)floor(x));
return 0;
}
当然也可以使用字符串。
C 只因出现一次的数字
发现数列的顺序与答案无关，所以我们可以对数字分类。
如何快速地对所有的数字分类呢？即把重复的数字放在一起。
可以哈希，不过，我们可以排序，这样的话，相同的元素必定是相邻的，只要忽略掉与相邻元素相同的元素，剩下的输出，就能找到“只因出现一次的数字 ”。
注意考虑 i=1 和 i=n 的情况。
#include <bits/stdc++.h>
using namespace std;
int n, x[1000002];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &x[i]);
sort(x + 1, x + n + 1);
x[0] = -114514;
x[n + 1] = -1919810;
for (int i = 1; i <= n; ++i) {
if (x[i] != x[i - 1] && x[i] != x[i + 1]) {
printf("%d ", x[i]);
}
}
return 0;
}
难度稍微提上来了，稍加分析 K_a 就是 a 到 a 后面下一个更大的数字（没有可以记为 n+1）中间数字的个数，唯一关键的就是如何找到每个数下一个更大的数字。
可以使用单调栈来维护，简而言之，从 1 ~ n 依次加入单调栈中，但是如果待加入的元素大于栈顶元素，说明这个栈顶元素下一个更大的数字就是自己，更新栈顶元素的答案，然后踢出他，重复执行直到栈空或不满足条件即可。
由于每一个元素最多进栈一次，出栈一次，所以时间复杂度为 O(n)。
#include <bits/stdc++.h>
using namespace std;
int n, a[800002];
int ans[800002], st[800002], top;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
while (a[i] >= a[st[top]] && top) {
ans[st[top--]] = i;
}
st[++top] = i;
}
while (st[top]) ans[st[top--]] = n + 1;
long long sum = 0;
for (int i = 1; i <= n; ++i) {
sum += ans[i] - i - 1;
}
printf("%lld\n", sum);
return 0;
}
E 可恶的 zhangjinxuan
这并没有我们想象的那样复杂。
因为直接求有相邻的非常不好求，而且还要套容斥，不如先考虑不会产生矛盾的。
如果一组方案不会产生矛盾，那么这个方案一定是这样的：
1 . 第一个团队任意，一共 N 种选择
2 . 第二个团队不能和第一个团队相同，只有 N-1 种选择。
...
i . 第 $i$ 个团队不能和第 i-1 个团队相同，只有 N-1 种选择。
...
M. 第 $M$ 个团队不能和第 M-1 个团队相同，只有 N-1 种选择。
所以不会产生矛盾的方案数就是 (M-1)^(N-1) * N
而所有可能的做题方案就是 M^N 种，所以最终的答案就是 M^N-(M-1)^(N-1) * N。
不想贴代码，C++ 只要注意一下负数取模就可以了。
B2 高斯记号
比较复杂，而且还有小数运算，更没有 spj，考虑 Python。
前面的处理都是模拟，直接贴代码：
def floor(x):
return int(x) if x >= 0 else int(x) - 1
s = input().strip()
rs = str()
pos = 0
kuohao = -1
number = ''
for i in s:
if i == '[' or i == '{':
kuohao = 1
elif i == '}':
rs += str(float(number)- floor(float(number)))
number = ''
kuohao = -1
elif i == ']':
rs += str(floor(float(number)))
number = ''
kuohao = -1;
elif kuohao == -1:
rs += i
else:
number += i
ans = eval(rs)
if ans == int(ans):
print(int(ans))
else:
print(ans)
你说得对，但是 WA 46pts。
这很正常，因为这个是提取小数产生的误差，我们不应该用 $N - \lfloor N \rfloor$ 来获取小数部分，更好的替代方案是使用字符串：
def floor(x):
return int(x) if x >= 0 else int(x) - 1
s = input().strip()
rs = str()
pos = 0
kuohao = -1
number = ''
for i in s:
if i == '[' or i == '{':
kuohao = 1
elif i == '}':
rs += '0.'+number.split('.')[1]
number = ''
kuohao = -1
elif i == ']':
rs += number.split('.')[0]
number = ''
kuohao = -1;
elif kuohao == -1:
rs += i
else:
number += i
ans = eval(rs)
if ans == int(ans):
print(int(ans))
else:
print(ans)
F 公因数
感觉也没有这么难，也就是推式子：
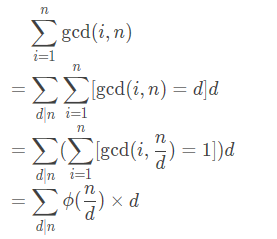
很简单有没有？
#include <bits/stdc++.h>
using namespace std;
long long phi(long long a) {
long long res = a;
for (long long i = 2; i * i <= a; ++i) {
if (a % i == 0) {
res = res * (i - 1) / i;
while (a % i == 0) {
a /= i;
}
}
}
if (a > 1) res = res * (a - 1) / a;
return res;
}
int main() {
long long a;
scanf("%lld", &a);
long long res = 0;
for (long long i = 1; i * i <= a; ++i) {
if (a % i == 0) {
res += phi(a / i) * i;
if (i * i != a) {
res += phi(i) * (a / i);
}
}
}
printf("%lld\n", res);
return 0;
}
时间复杂度证明：
枚举 N 的因数，\sqrt{N} 时间复杂度。
N 大约有 log N 个因数，对于每一个因数，都需要用 sqrt{N} 的复杂度求解，所以最终时间复杂度为 O(sqrt{N} log N。
在 N 为 2^32 量级可以通过。
题目总结（验题人主观评价）
也是很均匀的，题目质量很高。
| 题目编号 | 题目难度 | 算法标签 | 个人评价
| | A | 入门 | 模拟 | 简单阅读题
| | B1 | 入门 | 字符串 | 简单字符串题
| | C | 普及- | 排序，哈希 | 简单思维题
| | D | 普及 | 单调栈 | 简单模板题
| | E | 普及 | 数学 | 简单计数题
| | B2 | 普及+ | 字符串 | 中等字符串题
| | F | 提高- | 数学 | 中等数学题 |
好了，这就是 FCOI #11 的全部题目的题解，完工，散会！
|
评分
-
| 参与人数 5 | 荣誉 +20 |
鱼币 +21 |
贡献 +15 |
收起
理由
|
 鱼小二
| + 4 |
+ 5 |
+ 3 |
鱼C有你更精彩^_^ |
 陶远航
| + 5 |
+ 5 |
+ 3 |
感谢楼主无私奉献！ |
 小甲鱼
| + 6 |
+ 6 |
+ 6 |
鱼C有你更精彩^_^ |
 python爱好者.
| + 5 |
|
+ 3 |
鱼C有你更精彩^_^ |
 中英文泡椒
| |
+ 5 |
|
无条件支持楼主！ |
查看全部评分
|
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2023-12-1 12:50:55
置顶卡
千斤顶
显身卡
发表于 2023-12-1 18:52:44
楼主
发表于 2023-12-2 05:10:47