|
|
马上注册，结交更多好友，享用更多功能^_^
您需要 登录 才可以下载或查看，没有账号？立即注册
x
看到一个算法问题，说的是:
有一个m*n的矩阵格子，里面每个格子有一个正数，一个人从左上要走到右下，每次只能往右或者下走，每经过一个格子他就拿走其分数，拿了格子里面的分数就没有了（为0），求如何走让分数最大。以下是难度：这个人这么走了2次，求怎么走让2次的总和最大。
思路:
先来走一次的，这个比较好写。
三种方法因为只能走右或下，所以选择两个中最大的来走。
第一种也就是贪婪的写法。
def tl(seq):
count1,count2 = [],[]
results = []
def move(seq,a = [0,0],result = 0,remove = []):
if a == [len(seq)-1,len(seq[0])-1]:
count1.append(result)
count2.append(remove)
else:
if a[0] == len(seq)-1:
move(seq,a = [a[0],a[1]+1],result = result+seq[a[0]][a[1]] ,remove = remove + [a])
elif a[1] == len(seq[0])-1:
move(seq,a = [a[0]+1,a[1]],result = result+seq[a[0]][a[1]],remove = remove + [a])
else:
if seq[a[0]][a[1]+1] < seq[a[0]+1][a[1]]:
move(seq,a = [a[0]+1,a[1]],result = result+seq[a[0]][a[1]],remove = remove + [a])
else:
move(seq,a = [a[0],a[1]+1],result = result+seq[a[0]][a[1]],remove = remove + [a])
move(seq)
[
[0,3,4,5,6],
[1,2,3,4,5],
[5,6,7,8,1],
[3,5,6,7,0]
]
这也就是只贪图眼前，而不够长远的做法，所以想解决问题还是不要贪婪！
第二种方法，暴力随机数。
想拼人品就把次数弄少点，想全点就把次数弄多点。
此方法太过暴力，慎用！
想试试的看一下这个问题。当时我用的随机数，那效率，没的说~，低到爆- -。
http://bbs.fishc.com/forum.php?m ... d=54578&ctid=12
第三种方法，动态规划。
动态规划是比较好的解决最优问题的方法，
也就是每走一步将结果暂存再将结果的可能性都列出，之后求最大。(不知道理解的对不对。)
将贪婪的修改一下就可以用啦。def dp(seq):
count1,count2 = [],[]
results = []
def move(seq,a = [0,0],result = 0,remove = []):
if a == [len(seq)-1,len(seq[0])-1]:
count1.append(result)
count2.append(remove)
else:
if a[0] == len(seq)-1:
move(seq,a = [a[0],a[1]+1],result = result+seq[a[0]][a[1]] ,remove = remove + [a])
elif a[1] == len(seq[0])-1:
move(seq,a = [a[0]+1,a[1]],result = result+seq[a[0]][a[1]],remove = remove + [a])
else:
move(seq,a = [a[0],a[1]+1],result = result+seq[a[0]][a[1]],remove = remove + [a])
move(seq,a = [a[0]+1,a[1]],result = result+seq[a[0]][a[1]],remove = remove + [a])
move(seq)
当然也可以用迭代来完成，用迭代可能要嵌套多个循环，能理出头绪就试试吧~。
---------------------------------------凶残的化身----------------------暴力分割线--------------------------------------
回到问题，上面只是解决了一步，
P.S(我是问题: 有一个m*n的矩阵格子，里面每个格子有一个正数，一个人从左上要走到右下，每次只能往右或者下走，每经过一个格子他就拿走其分数，拿了格子里面的分数就没有了（为0），求如何走让分数最大。以下是难度：这个人这么走了2次，求怎么走让2次的总和最大。)
让第一次的最优了，那剩下的直接替换掉路径，再来一次最优那不就完成了！OK，说干就干。
加上 a = max(count1)
b = count2[count1.index(a)]
for i in range(len(b)):
seq[b[i][0]][b[i][1]] = 0
results.append(a)
count1,count2 = [],[]
move(seq)
results.append(max(count1))
[
[0,3,0,2],
[0,3,0,0],
[0,3,0,0],
[0,0,0,4],
[0,0,0,4],
[0,3,0,0]]
[17, 3]
也就是20，方法是动态规划本身是求的最优，应该是最优解了吧~。那他是怎么得来的呢?
第一次
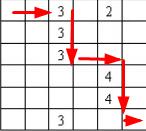，那第二次要么取3，要么取2，所以取了3。这样应该就最大了吧。
但是还有一种可以全取到的走法。(不唯一。)
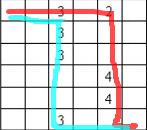
这样的结果是 22。显然最优。
现在问题来了:
我要说的显然不是如何编写最优解让挖掘鸡获取最大的效率T~T。(中国山东找蓝翔！)
动态规划还不能最优?
[url=]代码[/url]
其实是犯了一个错误，动态规划是整体上解决，但是我们是分步来看，局部动态规划，整体上就成了贪婪。谨慎！
 不过，我没写出来直接求解的答案，只会后面进行处理。
for i in range(len(count1)):
for c in range(len(count1[i:])):
temp = count1[i]+count1[c]
#将每一步的结果两两相加。
for j in range(len(count2[0])):
if count2[i][j] == count2[c][j]:
temp -= seq[count2[i][j][0]][count2[i][j][1]]
#重复的地方减少一个
results.append(temp)
少鱼币的童鞋，
练思路的童鞋，
来捧场的童鞋，
只有鱼币奖励- -。
是时候展示你犀利的思路，风骚的代码了！。
(more and more fish money!)
砖
玉:
|
评分
-
查看全部评分
|
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2014-12-8 15:05:47
置顶卡
千斤顶
显身卡
发表于 2014-12-8 15:20:19
楼主
叫你不当，吃亏了吧。