#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#define MaxSize 100
#define MaxWith 50
typedef int KeyType;
typedef char InfoType;
/*定义各节点的类型*/
typedef struct node
{
KeyType key; /*关键字项*/
int bf; /*增加的平衡因子*/
InfoType data; /*其它的数据与域*/
struct node *lchild; /*左孩子指针*/
struct node *rchild; /*右孩子指针*/
}AVLNode; /*AVL树中节点类型定义*/
int m = 0;
AVLNode *b = NULL; /*定义全局变量m、*b*/
/*左平衡旋转情况处理*/
void LeftProcess(AVLNode *&p, int &taller)
{
AVLNode *p1, *p2;
if (p->bf == 0) /*当左右子树等高时插入使树高度增加*/
{
p->bf = 1;
taller = 1; /*所以平衡因子置为1，高度为1*/
}
else if (p->bf == -1) /*当右子树比左子树高，插入后左右子树等高*/
{
p->bf = 0;
taller = 0; /*所以平衡因子置为0，高度为0*/
}
else /*当左子树比右子树高时插入则需做左平衡处理*/
{
p1 = p->lchild;
if (p1->bf == 1) /*当插入到左孩子的左子树上时需做LL处理*/
{
p->lchild = p1->rchild;
p1->rchild = p;
p->bf = p1->bf = 0;
p = p1;
}
else if (p1->bf == -1) /*当插入到左孩子的右子树上时需做LR处理*/
{
p2 = p1->rchild;
p1->rchild = p2->lchild;
p2->lchild = p1;
p->lchild = p2->rchild;
p2->rchild = p;
p = p2; /*将p指向新的根节点，并置bf的值为0*/
p->bf = 0;
}
taller = 0;
}
}
/*右平衡旋转情况处理*/
void RightProcess(AVLNode *&p, int &taller) /*操作类似上面，请参照左平衡旋转处理*/
{
AVLNode *p1, *p2;
if (p->bf == 0)
{
p->bf = -1;
taller = 1;
}
else if (p->bf == 1)
{
p->bf = 0;
taller = 0;
}
else
{
p1 = p->rchild;
if (p1->bf == -1)
{
p->rchild = p1->lchild;
p1->lchild = p;
p->bf = p1->bf = 0;
p = p1;
}
else if (p1->bf == 1)
{
p2 = p1->lchild;
p1->lchild = p2->rchild;
p2->rchild = p1;
p->rchild = p2->lchild;
p2->lchild = p;
p = p2;
p->bf = 0;
}
taller = 0;
}
}
/*在进行删除平衡二叉树的节点时候需要做相应的左平衡旋转处理*/
void LeftProcess1(AVLNode *&p, int &taller)
{
AVLNode *p1, *p2;
if (p->bf == 1)
{
p->bf = 0;
taller = 1;
}
else if (p->bf == 0)
{
p->bf = -1;
taller = 0;
}
else
{
p1 = p->rchild; /*RR处理*/
if (p1->bf == 0)
{
p->rchild = p1->lchild;
p1->rchild = p;
p1->bf = 1;
p->bf = -1;
p = p1;
taller = 0;
}
else if (p1->bf == -1) /*RR处理*/
{
p->rchild = p1->lchild;
p1->lchild = p;
p->bf = p1->bf = 0;
p = p1;
taller = 1;
}
else /*RL处理*/
{
p2 = p1->lchild;
p1->lchild = p2->rchild;
p2->rchild = p1;
p->rchild = p2->lchild;
p2->lchild = p;
p2->bf = 0;
p = p2;
taller = 1;
}
}
}
/*在进行删除平衡二叉树的节点时候需要做相应的右平衡旋转处理*/
void RightProcess1(AVLNode *&p, int &taller)
{
AVLNode *p1, *p2;
if (p->bf == -1)
{
p->bf = 0;
taller = -1;
}
else if (p->bf == 0)
{
p->bf = 1;
taller = 0;
}
else /*LL处理*/
{
p1 = p->lchild;
if (p1->bf == 0)
{
p->lchild = p1->rchild;
p1->rchild = p;
p->bf = -1;
p1->bf = 1;
p = p1;
taller = 0;
}
else if (p1->bf == 1) /*LL处理*/
{
p->lchild = p1->rchild;
p1->rchild = p;
p->bf = p1->bf = 0;
p = p1;
taller = 1;
}
else /*LR处理*/
{
p2 = p1->rchild = p2->lchild;
p2->lchild = p1;
p->lchild = p2->rchild;
p2->rchild = p;
p2->bf = 0;
p = p2;
taller = 1;
}
}
}
void Delete2(AVLNode *q, AVLNode *&r, int &taller) /*用于被删除节点左右子树均不为空*/
{
if (r->rchild == NULL)
{
q->key = r->key;
q = r;
r = r->lchild;
free(q);
taller = 1;
}
else
{
Delete2(q, r->rchild, taller);
if (taller == 1)
RightProcess(r, taller);
}
}
/*删除平衡二叉树的节点*/
int DeleteAVL(AVLNode *&p, KeyType x, int &taller)
{
int k;
AVLNode *q;
if (p == NULL) /*如果为空树，则正常退出*/
return 0;
else if (x < p->key) /*如果待删除的节点小于该节点，则往它左孩子寻找*/
{
k = DeleteAVL(p->lchild, x, taller);
if (taller == 1) /**/
LeftProcess(p, taller);
return k;
}
else if (x > p->key)
{
k = DeleteAVL(p->rchild, x, taller);
if (taller == 1)
RightProcess1(p, taller);
return k;
}
else
{
q = p;
if (p->rchild == NULL) /*被删节点右子树为空*/
{
p = p->lchild;
free(q);
taller = 1;
}
else if (p->rchild == NULL) /*被删节点左子树为空*/
{
p = p->lchild;
free(q);
taller = 1;
}
else /*被删节点左右子树均不为空*/
{
Delete2(q, q->lchild, taller);
if (taller == 1)
LeftProcess1(q, taller);
p = q;
}
return 1;
}
}
/*销毁平衡二叉树*/
void DestroyAVL(AVLNode *&b)
{
if (b->lchild)
DestroyAVL(b->lchild);
if (b->rchild)
DestroyAVL(b->rchild);
free(b);
b = NULL;
}
/*向当前平衡二叉树插入一个元素*/
int InsertNode(AVLNode *&b, KeyType e, int &taller)
{
if (b == NULL) /*当b为空树时进行动态分配等待插入新元素*/
{
b = (AVLNode *)malloc(sizeof(AVLNode));
b->key = e;
b->lchild = b->rchild = NULL;
b->bf = 0; /*将平衡因子置为 0*/
taller = 1; /*将该节点的高度置为 1*/
}
else
{
if (e == b->key) /*如果树中已经存在该点，则无需插入*/
{
taller = 0;
return 0;
}
if (e < b->key) /*如果待插入的数小于该节点，则往它左孩子插入*/
{
if ((InsertNode(b->lchild, e, taller)) == 0)
return 0;
if (taller == 1) /*若该节点的高度为1，插入后增1，则会破坏平衡*/
LeftProcess(b, taller); /*破坏后进行左平衡旋转处理重新达到平衡*/
}
else /*否则往它右孩子插入*/
{
if ((InsertNode(b->rchild, e, taller)) == 0)
return 0;
if (taller == 1) /*若该节点的高度为1，插入后增1，则会破坏平衡*/
RightProcess(b, taller); /*破坏后进行右平衡旋转处理重新达到平衡*/
}
}
return 1;
}
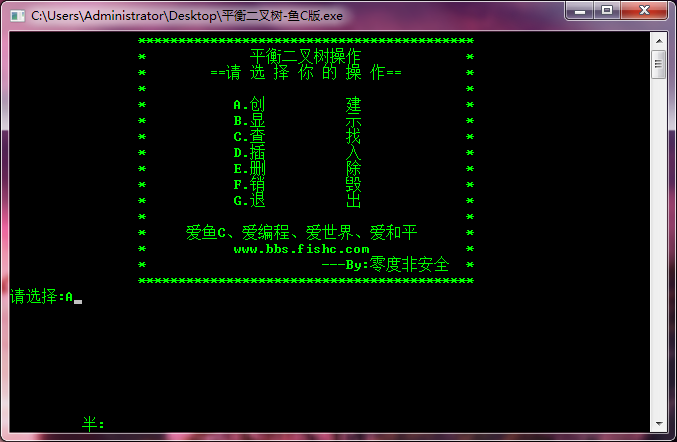
/*输出要选择操作的功能菜单*/
void OutputAVL(AVLNode *b)
{
system("cls");
system("color a");
printf("\t\t******************************************\n");
printf("\t\t* 平衡二叉树操作 *\n");
printf("\t\t* ==请 选 择 你 的 操 作== *\n");
printf("\t\t* *\n");
printf("\t\t* A.创 建 *\n");
printf("\t\t* B.显 示 *\n");
printf("\t\t* C.查 找 *\n");
printf("\t\t* D.插 入 *\n");
printf("\t\t* E.删 除 *\n");
printf("\t\t* F.销 毁 *\n");
printf("\t\t* G.退 出 *\n");
printf("\t\t* *\n");
printf("\t\t* 爱鱼C、爱编程、爱世界、爱和平 *\n");
printf("\t\t* www.bbs.fishc.com *\n");
printf("\t\t* ---By:零度非安全 *\n");
printf("\t\t******************************************\n");
}
/*递归查找平衡二叉树中的元素*/
bool SearchAVLNode(AVLNode *&b, int n)
{
if (!b)
return false;
else if (n == b->key) /*找到了返回true*/
return true;
else if (n < b->key)
return SearchAVLNode(b->lchild, n); /*如果小于则继续在其左孩子中查找*/
else
return SearchAVLNode(b->rchild, n); /*否则就到右孩子中查找*/
}
/*打印平衡二叉树的状态*/
void PrintAVLNode(AVLNode *b)
{
AVLNode *p, *St[MaxSize];
int level[MaxSize][2], top, n, i, width = 4;
if (b != NULL)
{
top = 1;
St[top] = b; /*将根节点入栈*/
level[top][0] = width;
while (top > 0)
{
p = St[top];
n = level[top][0];
for (i = 1; i <= n; i++)
printf(" ");
printf("%d", p->key);
for (i = n + 1; i < MaxSize - 6; i += 2)
printf("*");
printf("\n");
top--;
if (p->rchild != NULL) /*将右孩子根节点入栈*/
{
top++;
St[top] = p->rchild;
level[top][0] = n + width;
}
if (p->lchild != NULL) /*将左孩子根节点入栈*/
{
top++;
St[top] = p->lchild;
level[top][0] = n + width;
}
}
}
}
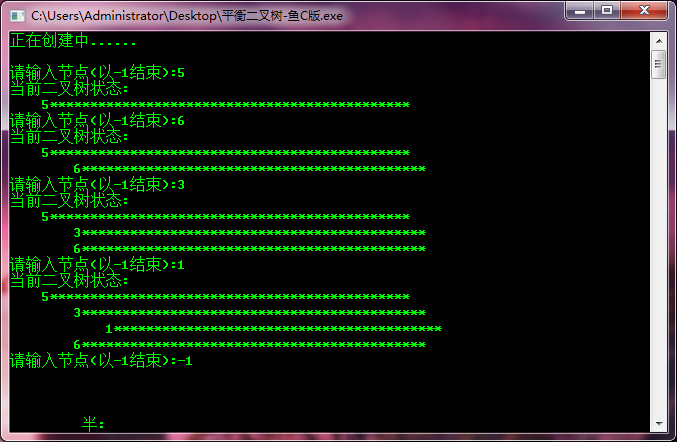
/*创建一个平衡二叉树*/
AVLNode *CreateAVL(AVLNode *&b)
{
int mainkey, i;
b = NULL;
printf("请输入节点(以-1结束):");
scanf("%d", &mainkey);
while (mainkey != -1) /*当输入的数不为-1时进行循环*/
{
InsertNode(b, mainkey, i);
printf("当前二叉树状态:\n");
PrintAVLNode(b);
printf("请输入节点(以-1结束):");
scanf("%d", &mainkey);
}
return b;
}
/*主函数*/
int main()
{
int node, h;
char ch; /*定义一个输入变量*/
while (1) /*进行循环操作*/
{
OutputAVL(b);
printf("请选择:");
ch = getchar();
fflush(stdin); /*清除输入的缓存*/
if (ch == 'A') /*进行创建操作*/
{
system("cls");
printf("正在创建中......\n\n");
CreateAVL(b);
system("pause");
}
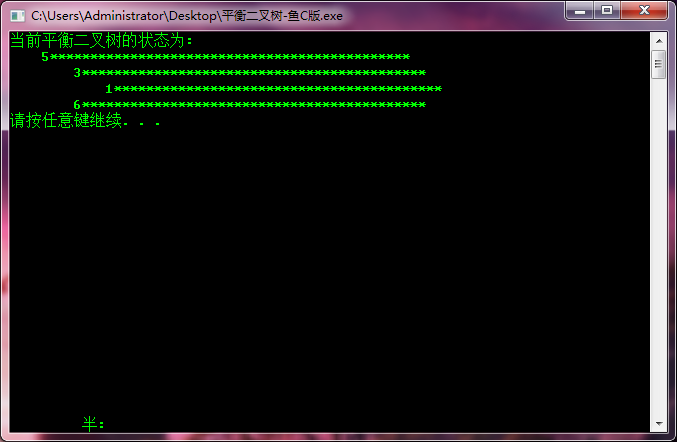
else if (ch == 'B') /*进行显示操作*/
{
system("cls");
printf("当前平衡二叉树的状态为:\n");
PrintAVLNode(b);
system("pause");
}
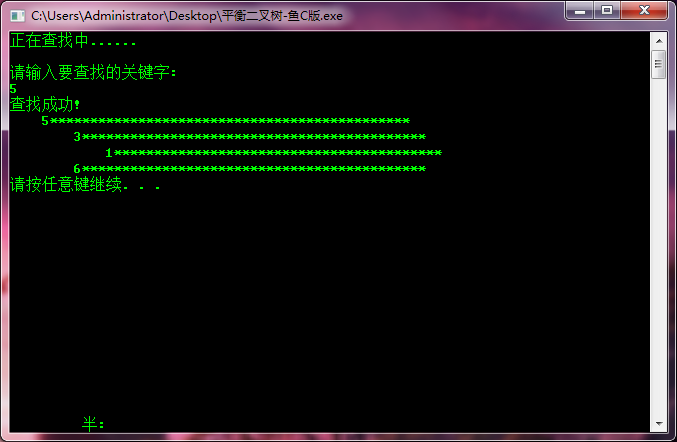
else if (ch == 'C') /*进行查找操作*/
{
system("cls");
printf("正在查找中......\n\n");
printf("请输入要查找的关键字:\n");
scanf("%d", &node);
if (SearchAVLNode(b, node))
{
printf("查找成功!\n");
PrintAVLNode(b); /*当查找成功时输出当前平衡二叉树的状态*/
}
else
{
printf("查找失败!\n");
printf("当前平衡二叉树中根本不存在这个节点\n"); /*当查找失败提示用户这树中不存在该节点*/
}
system("pause");
}
else if (ch == 'D') /*进行插入操作*/
{
system("cls");
printf("正在插入中......\n\n");
printf("请输入关键字(整数):\n");
scanf("%d", &node);
InsertNode(b, node, h);
system("pause");
}
else if (ch == 'E') /*进行删除操作*/
{
system("cls");
printf("正在删除中......\n\n");
printf("请输入关键字(整数):\n");
scanf("%d", &node);
if (DeleteAVL(b, node, h))
{
printf("删除成功!\n");
PrintAVLNode(b); /*当删除成功时及时显示当前平衡二叉树状态*/
}
else
printf("删除失败!\n");
system("pause");
}
else if (ch == 'F') /*进行销毁操作*/
{
system("cls");
printf("正在销毁中......\n\n");
DestroyAVL(b);
printf("销毁成功!\n");
system("pause");
}
else if (ch == 'G') /*进行退出操作*/
exit(0);
OutputAVL(b);
fflush(stdin);
}
return 0; /*程序正常退出*/
}
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2015-11-11 20:52:47
置顶卡
千斤顶
显身卡
楼主
发表于 2015-11-20 02:34:11
哈哈，看来还要想办法改进下课程~~
发表于 2015-11-21 20:41:15