|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
Product-sum numbers
A natural number, N, that can be written as the sum and product of a given set of at least two natural numbers,
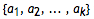 is called a product-sum number:
is called a product-sum number:
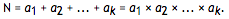
For example, 6 = 1 + 2 + 3 = 1 × 2 × 3.
For a given set of size, k, we shall call the smallest N with this property a minimal product-sum number. The minimal product-sum numbers for sets of size, k = 2, 3, 4, 5, and 6 are as follows.
Hence for 2≤k≤6, the sum of all the minimal product-sum numbers is 4+6+8+12 = 30; note that 8 is only counted once in the sum.
In fact, as the complete set of minimal product-sum numbers for 2≤k≤12 is {4, 6, 8, 12, 15, 16}, the sum is 61.
What is the sum of all the minimal product-sum numbers for 2≤k≤12000?
题目:
一个自然数N如果能写成一个两个元素以上的集合,
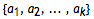 ,中元素的积与和的话,该数字被称为积和数:
,中元素的积与和的话,该数字被称为积和数:
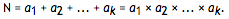
例如:6 = 1 + 2 + 3 = 1 × 2 × 3.
对于一个大小为 k 的集合,我们将最小的具有该性质的数字 N 成为一个最小积和数。k = 2, 3, 4, 5, 6 的集合的最小积和数如下:
因此对于 2≤k≤6, 所有最小积和数的总和为 4+6+8+12 = 30;注意 8 在求和时只计算一次。
事实上对于 2≤k≤12,所有最小积和数的集合是 {4, 6, 8, 12, 15, 16},其和为 61。
对于 2≤k≤12000,所有最小积和数的和是多少?
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)