|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
本帖最后由 欧拉计划 于 2016-8-17 18:12 编辑
Optimum polynomial
If we are presented with the first k terms of a sequence it is impossible to say with certainty the value of the next term, as there are infinitely many polynomial functions that can model the sequence.
As an example, let us consider the sequence of cube numbers. This is defined by the generating function,
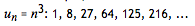
Suppose we were only given the first two terms of this sequence. Working on the principle that "simple is best" we should assume a linear relationship and predict the next term to be 15 (common difference 7). Even if we were presented with the first three terms, by the same principle of simplicity, a quadratic relationship should be assumed.
We shall define OP(k, n) to be the
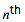 term of the optimum polynomial generating function for the first k terms of a sequence. It should be clear that OP(k, n) will accurately generate the terms of the sequence for n ≤ k, and potentially the first incorrect term (FIT) will be OP(k, k+1); in which case we shall call it a bad OP (BOP).
term of the optimum polynomial generating function for the first k terms of a sequence. It should be clear that OP(k, n) will accurately generate the terms of the sequence for n ≤ k, and potentially the first incorrect term (FIT) will be OP(k, k+1); in which case we shall call it a bad OP (BOP).
As a basis, if we were only given the first term of sequence, it would be most sensible to assume constancy; that is, for
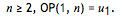
Hence we obtain the following OPs for the cubic sequence:

Clearly no BOPs exist for k ≥ 4.
By considering the sum of FITs generated by the BOPs (indicated in red above), we obtain 1 + 15 + 58 = 74.
Consider the following tenth degree polynomial generating function:
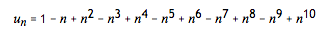
Find the sum of FITs for the BOPs.
题目:
如果给出一个序列的前 k 项,是不可能确定该序列的下一项的,因为有无限多个多项式函数可以模拟这个序列。
例如,我们考虑立方数序列。其生成函数为:
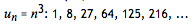
假设我们只知道该序列的前两项。遵循“简单的就是最好的”原则的话,我们应该用一个线性关系来预测下一个项,我们会得到 15(公差为 7)。即使我们知道了前三项,遵循同样的简单最优原则,我们也会使用二次函数的关系来预测下一项。
我们将 OP(k, n) 定义为一个序列前 k 项的最优生成函数的第 n 项。可知,对于 n ≤ k,OP(k, n) 能够准确地生成该序列中的项,而且第一个不正确的项(FIT)将会是 OP(k, k+1),在这种情况下我们将这一 OP 称为一个坏的 OP(BOP)。
如果我们只知道一个序列的第一项的话,最合理的方式就是认为这是一个常数数列;也就是说,对于
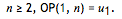
这样我们就得到立方数数列的如下 OP:

显然对于 k ≥ 4,不存在 BOP。
考虑 BOP 生成的 FIT(上面例子中红色的数字)之和,我们得到 1 + 15 + 58 = 74。
考虑如下的 10 阶多项式生成函数:
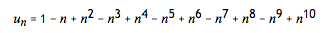
求该生成函数的 BOP 生成的 FIT 之和。
|
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)