题目105：找出文件中特殊和集之和

欧拉计划

Special subset sums: testing

Let S(A) represent the sum of elements in set A of size n. We shall call it a special sum set if for any two non-empty disjoint subsets, B and C, the following properties are true:

i. S(B) ≠ S(C); that is, sums of subsets cannot be equal.
ii. If B contains more elements than C then S(B) > S(C).

For example, {81, 88, 75, 42, 87, 84, 86, 65} is not a special sum set because 65 + 87 + 88 = 75 + 81 + 84, whereas {157, 150, 164, 119, 79, 159, 161, 139, 158} satisfies both rules for all possible subset pair combinations and S(A) = 1286.

Using sets.txt (right click and "Save Link/Target As..."), a 4K text file with one-hundred sets containing seven to twelve elements (the two examples given above are the first two sets in the file), identify all the special sum sets, 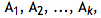and find the value of

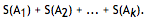
NOTE: This problem is related to Problem 103 and Problem 106.

题目：

用 S(A) 表示一个包含 n 个元素的集合 A 的元素之和。如果该集合的任意两个非空不相交子集满足以下性质，我们将其称为一个特殊和集。

i. S(B) ≠ S(C)； 也就是两个子集的和不相等。
ii. 如果 B 中的元素数量多于 C，则 S(B) > S(C)。

例如，{81, 88, 75, 42, 87, 84, 86, 65} 不是一个特殊和集，因为 65 + 87 + 88 = 75 + 81 + 84。而 {157, 150, 164, 119, 79, 159, 161, 139, 158} 的所有子集都满足上述两个条件，而且 S(A)=1286。

p105_sets.txt (3.55 KB, 下载次数: 7)

2016-8-17 22:44 上传

点击文件名下载附件

包含一千个集合，每个集合包含 7 到 12 个元素，找出所有的特殊和集 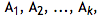并求

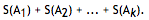
注意：该题目与题目 103， 106 相关。

jerryxjr1220

这题没有想到更好的思路，完全是暴力破解。
用itertools的combination库穷举所有组合加以比较。不过速度到还可以，比预想快很多，4秒钟也出结果了。
73702
[Finished in 4.2s]

with open('p105_sets.txt') as f:
        data = f.readlines()
sets = [[int(i) for i in d.strip('\n').split(',')] for d in data]
#print(sets)
def is_special(sets):
        from itertools import combinations
        if len(sets) != len(set(sets)):
                return False
        for num in range(1, len(sets)+1):
                for group in combinations(sets, num):
                        for j in range(1, len(sets)-num+1):
                                for others in combinations(list(set(sets)-set(group)), j):
                                        if sum(group) == sum(others):
                                                return False
                        for j in range(1,num):
                                for others in combinations(list(set(sets)-set(group)), j):
                                        if sum(group) <= sum(others):
                                                return False
        return True
A = []
for each_group in sets:
        if is_special(each_group):
                A.append(each_group)
print(sum((sum(a) for a in A)))

jerryxjr1220

这题用bruce force，没有更好的思路，利用itertools的combination穷举所有组合。
用时比预想要短，4秒钟也出答案了。
73702
[Finished in 4.2s]

with open('p105_sets.txt') as f:
        data = f.readlines()
sets = [[int(i) for i in d.strip('\n').split(',')] for d in data]
#print(sets)
def is_special(sets):
        from itertools import combinations
        if len(sets) != len(set(sets)):
                return False
        for num in range(1, len(sets)+1):
                for group in combinations(sets, num):
                        for j in range(1, len(sets)-num+1):
                                for others in combinations(list(set(sets)-set(group)), j):
                                        if sum(group) == sum(others):
                                                return False
                        for j in range(1,num):
                                for others in combinations(list(set(sets)-set(group)), j):
                                        if sum(group) <= sum(others):
                                                return False
        return True
A = []
for each_group in sets:
        if is_special(each_group):
                A.append(each_group)
print(sum((sum(a) for a in A)))