题目153：研究高斯整数

欧拉计划

Investigating Gaussian Integers

As we all know the equation x²=-1 has no solutions for real x.
If we however introduce the imaginary number i this equation has two solutions: x=i and x=-i.
If we go a step further the equation (x-3)²=-4 has two complex solutions: x=3+2i and x=3-2i.
x=3+2i and x=3-2i are called each others' complex conjugate.
Numbers of the form a+bi are called complex numbers.
In general a+bi and a-bi are each other's complex conjugate.

A Gaussian Integer is a complex number a+bi such that both a and b are integers.
The regular integers are also Gaussian integers (with b=0).
To distinguish them from Gaussian integers with b ≠ 0 we call such integers "rational integers."
A Gaussian integer is called a divisor of a rational integer n if the result is also a Gaussian integer.
If for example we divide 5 by 1+2i we can simplify 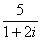  in the following manner:
Multiply numerator and denominator by the complex conjugate of 1+2i: 1-2i.
The result is .
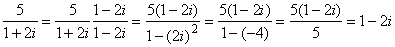So 1+2i is a divisor of 5.
Note that 1+i is not a divisor of 5 because .
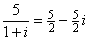Note also that if the Gaussian Integer (a+bi) is a divisor of a rational integer n, then its complex conjugate (a-bi) is also a divisor of n.

In fact, 5 has six divisors such that the real part is positive: {1, 1 + 2i, 1 - 2i, 2 + i, 2 - i, 5}.
The following is a table of all of the divisors for the first five positive rational integers:

For divisors with positive real parts, then, we have: .

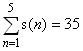For 1 ≤ n ≤ 10⁵, ∑ s(n)=17924657155.

What is ∑ s(n) for 1 ≤ n ≤ 10⁸?

题目：

正如我们所知，x²=-1 这个方程没有整数解

然而，如果我们引入虚数i，这个方程就有两个解：x=i 和 x=-i。

如果我们更进一步， (x-3)²=-4 有两个复数的解：x=3+2i 和 x=3-2i

x=3+2i 和 x=3-2i 互为复数的共轭

a+bi 这种形式的数字就是所谓的复数。一般来说，a+bi 和 a-bi 共轭。

高斯整数定义为：a 和 b都是整数的复数，a+bi。

实数（b=0）也是高斯整数，

为把实数和 b ≠ 0 的高斯整数区别开来，我们把这些整数叫做“有理整数”。

一个有理整数 n 除以一个高斯整数 P，所得的结果若也为高斯整数，那么，这个高斯整数 P 就被叫做 n 的除数。

比如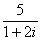， 我们可以按下面方式进行化简分子分母分别乘以 1+2i 的共轭数: 1-2i.
结果如下 .

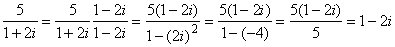所以，1+2i 是 5 的一个除数。

注意，1+i 不是 5 的除数，因为 .

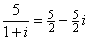另外还要注意：如果 (a+bi) 是有理整数 N 的除数，那么它的共轭数  (a-bi) 也是 N 的除数。

实际上，5 有六个除数，它们的实部都为正： {1, 1 + 2i, 1 - 2i, 2 + i, 2 - i, 5}。

下表显示了前五个正有理数具有的除数：

由这些实部为正的除数，我们可以得到和为 。

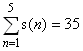对于 1 ≤ n ≤ 10⁵，∑ s(n)=17924657155

请问，对于 1 ≤ n ≤ 10⁸， ∑ s(n) 是多少？

guosl

应用数论中的不定方程x^2+y^2=n的正整数解来解决这个问题。且应用数论中的这个结论：某个正整数是两平方数之和，当且仅当该正整数的所有 4k+3 型素因子的幂次均为偶数。

加餐

直接考虑数n在这个范围maxn内可能成为的次数. 反向记录储存.

瓦屋青衣

import time
import math

timeStart = time.time()

n = 10**8

ans = 0

def sumOfDivisor(n:int) -> int:
    ans = 0
    m = int(n**0.5)
    for x in range(1, m+1):
        a = n//(x+1)+1
        b = n//x
        ans += (n//x + (a+b)*(b-a+1)//2) * x
    if m*(m+1) > n:
        ans -= m*m
    return ans

ans = sumOfDivisor(n)
m = int(n**0.5)
dic = {1:1}
for x in range(1, m+1):
    for y in range(1, int((n-x*x)**0.5)+1):
        if math.gcd(x, y) > 1:
            continue
        c = n//(x*x+y*y)
        if c in dic:
            s = dic[c]
        else:
            s = sumOfDivisor(c)
            dic[c] = s
        ans += 2*x*s

print(ans)

print(f'time used: {time.time() - timeStart: .3f} s')