|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
有详细的注释, 希望能给不明白的朋友提供帮助
源代码:
/*
**用递归求解八皇后问题
*/
#include <stdio.h>
#define SIZE 8 //皇后的个数 初始皇后的个数应 > 0
//修改SIZE就能实现n皇后问题的求解啦!
void EightQueens(int num);
//局部变量 被每层递归函数所共享
//也可以以指针的形式作为参数传参, 但考虑到每层递归函数都要传参,
//所以这里我设置成了局部变量
int count = 0; //记录解法的个数
int position[SIZE][2]; //皇后被安放的坐标(每行为一个坐标(横坐标, 纵坐标))
int map[SIZE][SIZE] = {0}; //表示棋盘, 值为0表示该位为空, 值为1表示该位已有皇后
int main()
{
EightQueens(SIZE); //皇后的个数
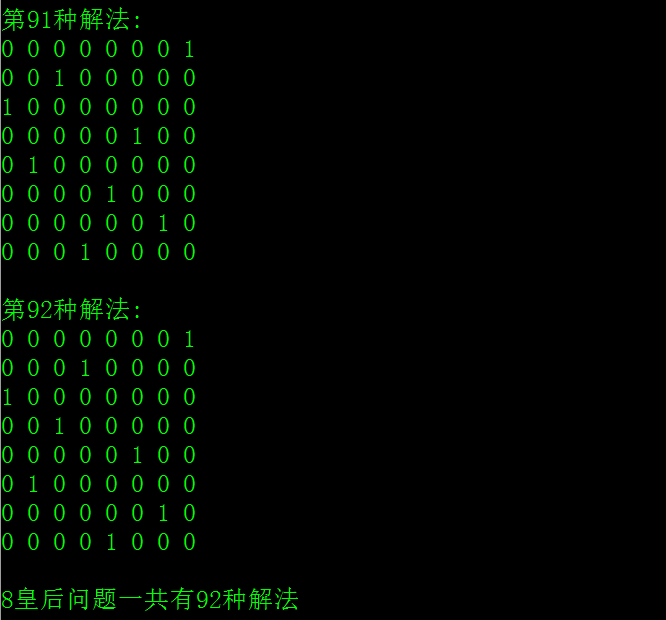
printf("%d皇后问题一共有%d种解法\n", SIZE, count);
return 0;
}
void EightQueens(int num)
{
int i, j;
int flag; //判断该位是否能作为皇后存放位的标志位, 1表示可以存放
if(num == 0)
{
count++; //成功找到一种解法
//打印此种解法的皇后安放情况(这里也可以输出position, 也就是皇后被安放的坐标)
//但为了直观我打印了棋盘, 其实棋盘这个参数并不是必须的要有的(只要在大脑中有一个逻辑上的棋盘就可以了)
printf("第%d种解法:\n", count);
for(i = 0; i < SIZE; i++)
{
for(j = 0; j < SIZE; j++)
{
printf("%d ", map[i][j]);
}
printf("\n");
}
printf("\n");
}
else
{
//在一行中找到一个安全的位置并安放皇后, 如果安放不了则返回(回溯到上一层), 表示安放失败
//若安放成功则继续调用, 进行下一层的安放
//此时已经安放了SIZE - num个皇后, 当前安放行的行横坐标也为SIZE - num
for(i = 0; i < SIZE; i++)
{
flag = 1;
for(j = 0; j < SIZE - num; j++)
{
if(i == position[j][1]
|| SIZE - num + i == position[j][0] + position[j][1]
|| SIZE - num - i == position[j][0] - position[j][1]) //当前位置与已被安放位置在同一列或位于同一对角线上
{ //(a, b)和(c, d)两点, 当c + d == a + b 或 c - d == a - b时两点在一个对角 线上(分别为两个方向的对角线)
flag = 0; //设置当前位不可存放
break;
}
}
if(flag == 1)
{
map[SIZE - num][i] = 1; //安放皇后
position[SIZE - num][0] = SIZE - num; //记录已安放的坐标
position[SIZE - num][1] = i;
EightQueens(num - 1); //向下一层调用
map[SIZE - num][i] = 0; //恢复棋盘 (position并不用恢复, 因为每一层都会自动覆盖)
}
}
}
}
/*
总体上就是循环+递归对所有摆放的情况进行了穷举(如果安放成功就向下一层调用, 失败则回溯到上一层)
找到其中满足条件的情况
*/
运行截图(部分):
|
-
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)