题目255：近似平方根

欧拉计划

Rounded Square Roots

We define the rounded-square-root of a positive integer n as the square root of n rounded to the nearest integer.

The following procedure (essentially Heron's method adapted to integer arithmetic) finds the rounded-square-root of n:

Let d be the number of digits of the number n.
If d is odd, set x₀ = 2×10^(d-1)/2.
If d is even, set x₀ = 7×10^(d-2)/2.
Repeat:

        

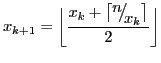
until x_k+1 = x_k.

As an example, let us find the rounded-square-root of n = 4321.
n has 4 digits, so x₀ = 7×10^(4-2)/2 = 70.
        

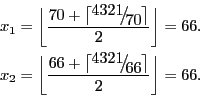
Since x₂ = x₁, we stop here.
So, after just two iterations, we have found that the rounded-square-root of 4321 is 66 (the actual square root is 65.7343137…).

The number of iterations required when using this method is surprisingly low.
For example, we can find the rounded-square-root of a 5-digit integer (10,000 ≤ n ≤ 99,999) with an average of 3.2102888889 iterations (the average value was rounded to 10 decimal places).

Using the procedure described above, what is the average number of iterations required to find the rounded-square-root of a 14-digit number (10¹³ ≤ n < 10¹⁴)?
Give your answer rounded to 10 decimal places.

Note: The symbols &#8970;x&#8971; and &#8968;x&#8969; represent the floor function and ceiling function respectively.

题目：

我们定义近似平方根为与 n 的平方根最接近的正整数。

下面的过程将得到 n 的近似平方根（本质上来说，这是将古希腊数学家海伦的方法应用到整数运算上）：

令 d 为数字 n 的数位。

如果 d 为奇数，令 x₀ = 2×10^(d-1)/2。
如果 d 为偶数，令 x₀ = 7×10^(d-2)/2。
重复：

        

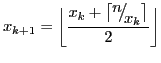
直到 x_k+1 = x_k。

例如，当我们来求 n = 4321 的近似平方根时。

由于 n 是 4 位数，d=4，所以 x₀ = 7×10^(4-2)/2 = 70。

         

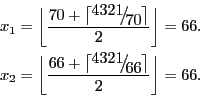
既然 x₂ = x₁，我们停止计算。

因此，在两次迭代后，我们得到 4321 的近似平方根为 66（事实上平方根为 65.7343137…）

使用这种方法所需要的迭代次数惊人的少。

例如，我们发现求 5 位数（10,000 ≤ n ≤ 99,999）的近似平方根所需的平均迭代次数为 3.2102888889 （平均值精确到小数点后 10 位）

使用上面介绍的方法，求 14 位数（10¹³ ≤ n < 10¹⁴）的近似平方根所需的平均迭代次数是多少？

答案精确到小数点后 10 位。


提示：符号 &#8970;x&#8971; 和 &#8968;x&#8969; 分别代表 x 的向下取整和向上取整。