matlab中有一个manova1函数，请问在python中对应哪个函数可以实现相同的功能？

TSUNAMI

以下是matlab中对应manova1的完整介绍，但是在python中不知道怎么实现，还请哪位大神能帮忙解决一下~


Syntax
d = manova1(X,group)
d = manova1(X,group,alpha)
[d,p] = manova1(...)
[d,p,stats] = manova1(...)

Description
d = manova1(X,group) performs a one-way Multivariate Analysis of Variance (MANOVA) for comparing the multivariate means of the columns of X, grouped by group. X is an m-by-n matrix of data values, and each row is a vector of measurements on n variables for a single observation. group is a grouping variable defined as a categorical variable, vector, character array, or cell array of character vectors. Two observations are in the same group if they have the same value in the group array. The observations in each group represent a sample from a population.

The function returns d, an estimate of the dimension of the space containing the group means. manova1 tests the null hypothesis that the means of each group are the same n-dimensional multivariate vector, and that any difference observed in the sample X is due to random chance. If d = 0, there is no evidence to reject that hypothesis. If d = 1, then you can reject the null hypothesis at the 5% level, but you cannot reject the hypothesis that the multivariate means lie on the same line. Similarly, if d = 2 the multivariate means may lie on the same plane in n-dimensional space, but not on the same line.

d = manova1(X,group,alpha) gives control of the significance level, alpha. The return value d will be the smallest dimension having p > alpha, where p is a p-value for testing whether the means lie in a space of that dimension.

[d,p] = manova1(...) also returns a p, a vector of p-values for testing whether the means lie in a space of dimension 0, 1, and so on. The largest possible dimension is either the dimension of the space, or one less than the number of groups. There is one element of p for each dimension up to, but not including, the largest.

If the ith p-value is near zero, this casts doubt on the hypothesis that the group means lie on a space of i-1 dimensions. The choice of a critical p-value to determine whether the result is judged statistically significant is left to the researcher and is specified by the value of the input argument alpha. It is common to declare a result significant if the p-value is less than 0.05 or 0.01.

[d,p,stats] = manova1(...) also returns stats, a structure containing additional MANOVA results. The structure contains the following fields.






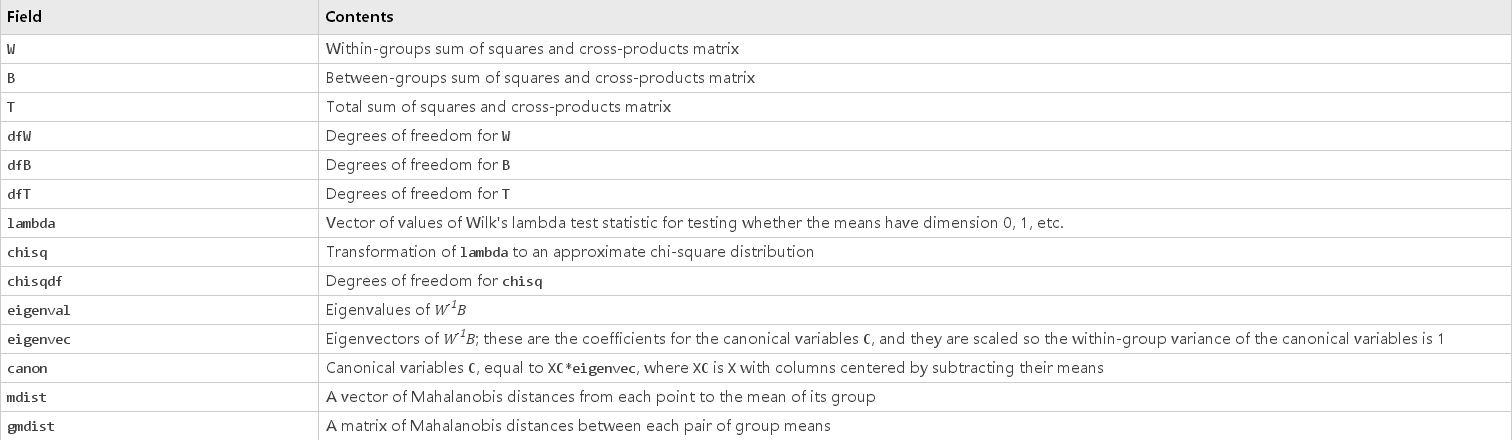
The canonical variables C are linear combinations of the original variables, chosen to maximize the separation between groups. Specifically, C(:,1) is the linear combination of the X columns that has the maximum separation between groups. This means that among all possible linear combinations, it is the one with the most significant F statistic in a one-way analysis of variance. C(:,2) has the maximum separation subject to it being orthogonal to C(:,1), and so on.

You may find it useful to use the outputs from manova1 along with other functions to supplement your analysis. For example, you may want to start with a grouped scatter plot matrix of the original variables using gplotmatrix. You can use gscatter to visualize the group separation using the first two canonical variables. You can use manovacluster to graph a dendrogram showing the clusters among the group means.

Assumptions
The MANOVA test makes the following assumptions about the data in X:

The populations for each group are normally distributed.
The variance-covariance matrix is the same for each population.
All observations are mutually independent.
Examples
you can use manova1 to determine whether there are differences in the averages of four car characteristics, among groups defined by the country where the cars were made.

load carbig
[d,p] = manova1([MPG Acceleration Weight Displacement],...
                Origin)
d =
   3
p =
     0
  0.0000
  0.0075
  0.1934
There are four dimensions in the input matrix, so the group means must lie in a four-dimensional space. manova1 shows that you cannot reject the hypothesis that the means lie in a 3-D subspace.

雪山凌狐

印象中R语言中有相应的函数

TSUNAMI

额，没有人知道吗？帖子都沉了呀。。。