|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
本帖最后由 超凡天赐 于 2017-6-9 20:18 编辑
小甲鱼老师已经说了关于插入排序,我们非常困惑关于时间是怎么分析出来的?这里再对插入排序
进行更深一步的数学分析。(这里并没有用到多么高深的数学知识,只不过是标题党罢了)
话不多说,先举个关于扑克牌的例子。
假如我们这里有十张牌。

我们来想象这个场景,我们先将十张牌放在桌子上,左手抽出第一张。下面我将用十分形象的方法来描述抽象的算法。注意看注释。
- //这里我们将分成两堆,一堆在左手上,另一堆在桌子上。我们不难发现其实左手上完全排序好的,桌子上是没有排序好的。
- #include <stdio.h>
- int main()
- {
- int i,j,right_hand;
- int card[10]={1,2,3,4,5,6,7,8,9,10};
- for(i=1;i<=9;i++)
- {
- right_hand=card[i];//这里我们将需要插入的牌从桌上放到右手上,此时我们左手已经有一张牌了(只有一张牌,当然排序好了)。
- j=i-1;//我们再把目标放到左手上。
- while(j>=0&&card[j]<right_hand)
- {
- card[j+1]=card[j];
- j--;
- }//在这里我们来想象一个动作,其实和我们平时理牌一个道理。我们拿右手上的牌和左手上最后一个牌先进行比较。如果右手上的牌大于左手上的牌,那么就将左手上最后一张牌向后移,倒数第二张还是这样,就还后移,直到找到合适的插入点。
- card[j+1]=right_hand;//这里为什么是j+1。其实这并不是逻辑上的问题,这是计算机指令的问题。因为这里最后j多减了一次1.
- }
- for(i=0;i<10;i++)
- printf("%d ",card[i]);
- return 0;
- }
仿佛算法就在眼前,摸得着,看得见。
分析算法:(见代码注释)
- //这里只对主要程序段进行时间分析
- //假设c是执行时间,n是执行次数
- #include <stdio.h>
- int main()
- {
- int i,j,right_hand;
- int card[10]={1,2,3,4,5,6,7,8,9,10};
- i=0;//c0
- while(i<=9)//c1 n=11
- {
- right_hand=card[i];//c2 n-1
- j=i-1;//c3 n-1
- while(j>=0&&card[j]<right_hand)//c4 1+2+···+n-1
- {
- card[j+1]=card[j];//c5 1+2+···+n-2
- j--;//c6 1+2+···+n-2
- }
- card[j+1]=right_hand;//c7 n-1
- i++;//c8 n-1
- }
- for(i=0;i<10;i++)
- printf("%d ",card[i]);
- return 0;
- }
好了,现在我们要进行求和,也就是求总时间。
我们先假设最坏情况,我写的那个C语言代码就是最坏情况。
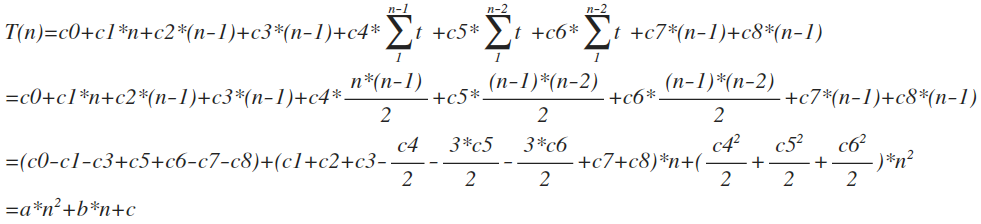
在这里,我们认为当n趋近于无穷大时,我们就可以认为这个算法的效率为n(o^2)
为什么?这里我来引入数学中的等价无穷大(其实这个是我瞎扯的,我没有找到什么依据)
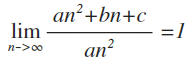
在分析算法效率时,我们总是把低阶的无穷大给扔掉,所谓低阶,是相对的,所以算法效率最差为n(o^2)
当最好的情况时呢?
回到上面的代码我们假设是排列好的,c4的执行次数就变成了n-1,所以这个算法效率最优为n(o);
那么平均呢?
这里就不用什么概率论了,就假设平均为一半比它大,一半比它小,c4的执行次数就变成了(1+2+···+n-1)/2,
我们再次按照上面的最差效率进行推导,
我们发现仍是o(o^2)!!!平均效率竟然和最差效率一样!!!!
这里其实还不是严格的数学证明,数学证明必须所有情况都成立才可以。 |
评分
-
| 参与人数 3 | 荣誉 +11 |
鱼币 +16 |
贡献 +11 |
收起
理由
|
 小甲鱼 小甲鱼
| |
+ 5 |
|
支持楼主! |
 零度非安全 零度非安全
| + 6 |
+ 6 |
+ 6 |
非常的nice |
 人造人 人造人
| + 5 |
+ 5 |
+ 5 |
热爱鱼C^_^ |
查看全部评分
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)