【每天进步一点点】Python解题笔记（06篇）

jerryxjr1220

明天要出差，今天就多写一篇吧。

继续来看“欧拉计划”的第6题：计算(1+2+3+...+100)^2与1^2+2^2+...+100^2的差。

其实，这题直接求解就可以，不需要什么数学知识，一行代码输出：

print(sum(range(1,101))**2-sum((i*i for i in range(1,101))))

不过这样就没啥好讲了，那么我们换个思路来看看。

如果把(1+2+3+...+100)^2展开会是什么？

如果一时想不出来的话，我们来看看这张图


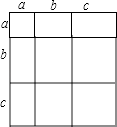
如果把(a+b+c)**2看成是大正方形的面积的话，那么它展开就是每个小矩形的面积之和.

那么一共有多少小矩形？ S=a^2+b^2+c^2+2*a*(b+c)+2*b*c

如果你能理解这个公式的话，那么推广到(1+2+3+..+100)^2 = 1^2+2^2+3^2+...+100^2+2*1*(2+3+...+100)+2*2*(3+4+..+100)+..+2*99*100应该就不难理解了吧。

这个展开式的前100项正好就是要被减去的，所以我们只需要求出2*1*(2+3+...+100)+2*2*(3+4+..+100)+..+2*99*100就可以了。

这个其实就是一个等差数列的求和公式，剩下就是累加了。

def multisum(start, end):
        return (start+end)*(end-start+1)//2
print(sum((2*i*multisum(i+1,100) for i in range(1, 100))))

是不是这样也能求解呢？

新手·ing

起一个很好想，Jerry下次把答案隐藏起来不是更好吗

jerryxjr1220

新手·ing 发表于 2017-9-5 21:59
起一个很好想，Jerry下次把答案隐藏起来不是更好吗

其实答案不是主要的，解题思路才是关键