马上注册，结交更多好友，享用更多功能^_^
您需要 登录 才可以下载或查看，没有账号？立即注册
x
本帖最后由 鱼C-小师妹 于 2021-12-11 14:29 编辑
在线讲解：
经过前面各种找数的洗礼，相信童鞋们的能力有了质的飞跃！
今天我们来一个很烧脑，但一旦理解就会发现很简单的：
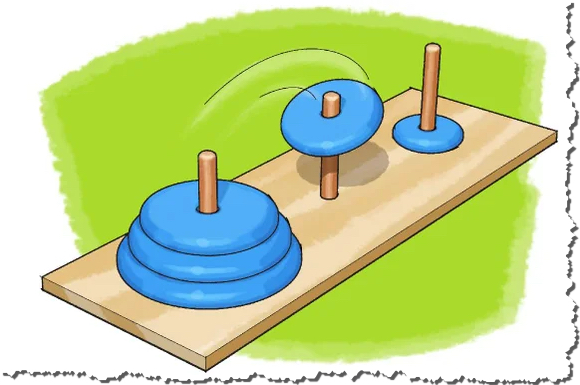
小师妹手中的这个玩具就是汉诺塔啦：
【去看视频哈】
汉诺塔是根据一个传说形成的数学问题。
在古代有一个梵塔，塔内有 A、B、C 三个座。
开始时 A 座上有 64 个盘子，盘子大小不同，但保证大的在下，小的在上。
现在有一个和尚想将这 64 个盘子从 A 座移动到 C 座。
他每次只能移动一个盘子，且在移动过程中在 3 个座上都必须保持大盘在下小盘在上的状态。
在移动过程中可以利用 B 座。
我们简化下上面的故事，A 座上有 N 个 (N>1) 穿孔圆盘，盘的尺寸由下到上依次变小。
要求按下列规则将所有圆盘移至 C 座：
接下来我们就通过编程将移动步骤打印出来！
首先考虑 A 座上最下面的盘子，如果能将它上面的 63 个盘子从 A 座移动到 C 座，则任务就完成了对不对。
具体步骤如下：
- 将 A 座最上面的 63 个盘子移动到 B 座上
- 将 A 座上剩下的一个盘子移动到 C 座上
- 将 B 座上的 63 个盘子移动到 C 座上
如果能完成上述 3 步，则任务完成。
这种思考方法就是递归的思考方法。
递归神马东东？？
传递一只龟龟吗？
哈哈，当然不是啦！
这里先引用小甲鱼老师的一句名言：
在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。
递归一词还较常用于描述以自相似方法重复事物的过程。
可以理解为自我复制的过程。
可以解决很多的计算机科学问题，因此它是计算机科学中十分重要的一个概念。
绝大多数编程语言支持函数的自调用，在这些语言中函数可以通过调用自身来进行递归。
计算机科学家尼克劳斯·维尔特如此描述递归：
递归的强大之处在于它允许用户用有限的语句描述无限的对象。因此，在计算机科学中，递归可以被用来描述无限步的运算，尽管描述运算的程序是有限的。
不愧是大神的描述，言简意赅却又玄妙入神～
让我们继续回到本讲的汉诺塔～
上面的 3 步实际上并没有解决问题，在步骤 1 中如何将 A 座最上面的 63 个盘子移动到 B 座上呢？
为了解决将将 A 座最上面的 63 个盘子移动到 B 座上的问题，还需要做如下工作：
- 将 A 座上面的 62 个盘子移动到 C 座上
- 将 A 座上剩下的一个盘子移动到 B 座上
- 将 C 座上的 62 个盘子移动到 B 座上
我们将这个过程进行下去，即不断地递归，继续完成移动 62 个盘子、61 个盘子……的工作。
直到最后达到仅有一个盘子的情形，则将一个盘子从一个座移动到另一个座，问题也就全部得到了解决。
所有的步骤都是可执行的。
要说明的是，只有移动一个盘子的任务完成后，移动两个盘子的任务才能完成。
以此类推，只有移动 63 个盘子的任务完成后，移动 64 个盘子的任务才能完成。
由此可知该问题是非常典型的递归问题。
基于上面的描述我们可以知道递归算法的一些特征：
为了求解规模为 N 的问题，应先设法将该问题分解成一些规模较小的问题，从这些较小问题的解可以方便地构造出大问题的解。同时，这些规模较小的问题也可以采用同样的方法分解成规模更小的问题，并能从这些规模更小的问题的解中构造出规模较小问题的解。特别地，当 N=1 时，可直接获得问题的解。
现在我们来找出解决问题的方法。
先定义递归函数 hanoi(N,A,B,C)，该方法表示将 N 个盘子从 A 座借助 B 座移动到 C 座，盘子的初始个数为 N。
步骤：
- 若 A 座上只有 1 个盘子，此时 N=1，则可直接将盘子从 A 座移动到 C 座上，问题得到解决。
- 若 A 座上有 1 个以上的盘子，即 N>1，此时需要再考虑 3 个步骤：
- 先将 N-1 个盘子从 A 座借助 C 座移动到 B 座上。显然，这 N-1 个盘子不能作为一个整体移动，而是要按照要求来移动。此时，可递归调用函数 hanoi(N-1,A,C,B)。需要注意的是，这里借助 C 座将 N-1 个盘子从 A 座移动到 B 座，A 是源，B 是目标。
- 将 A 座上剩下的第 N 个盘子移动到 C 座上。
- 将 B 座上的 N-1 个盘子借助 A 座移动到 C 座上。此时，递归调用函数 hanoi(N-1,B,A,C)。需要注意的是，这里借助于 A 座将 N-1 个盘子从 B 座移动到 C 座，B 是源，C 是目标。
- 完成了这 3 步，就可以实现预期的效果，在 C 座上按照正确的次序叠放好所有的盘子。
我们先用这 4 个盘子的案例来演示下过程：
【哈哈哈，去看视频】
根据前面的分析，编写递归函数 hanoi(N,A,B,C)：
def hanoi(N, A, B, C):
if N == 1: # 将A座上剩下的第N个盘子移动到C座上
print("将盘子 {} 从 {} 移到 {} ".format(N, A, C))
else:
hanoi(N-1, A, C, B) # 借助C座将N-1个盘子从A座移动到B座
print("将盘子 {} 从 {} 移到 {} ".format(N, A, C))
hanoi(N-1, B, A, C)
源码：
py20.py.zip
(396 Bytes, 下载次数: 16, 售价: 8 鱼币)
代码是不是超级简单！
这就是为什么说得递归者得天下的原因，童鞋们一定要好好消化～
假设你输入 64 个盘子，小师妹强烈不建议你这么做
（这么做的，请稍后过来扣 1）
因为移动次数是：
即使使用计算机也很难计算64层的汉诺塔问题哦～
记住千万不要多想，不要像人类一样整体来看，盲人摸象即可。
下课！ | 
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2021-8-9 19:48:24
置顶卡
千斤顶
显身卡
沙发~
发表于 2021-8-9 20:00:18
楼主
发表于 2021-8-10 10:41:24
