[已解决]唔，一个百思不得其解的树状树状题目相关的问题

御坂19090 · 发表于 2023-6-12 18:19:39

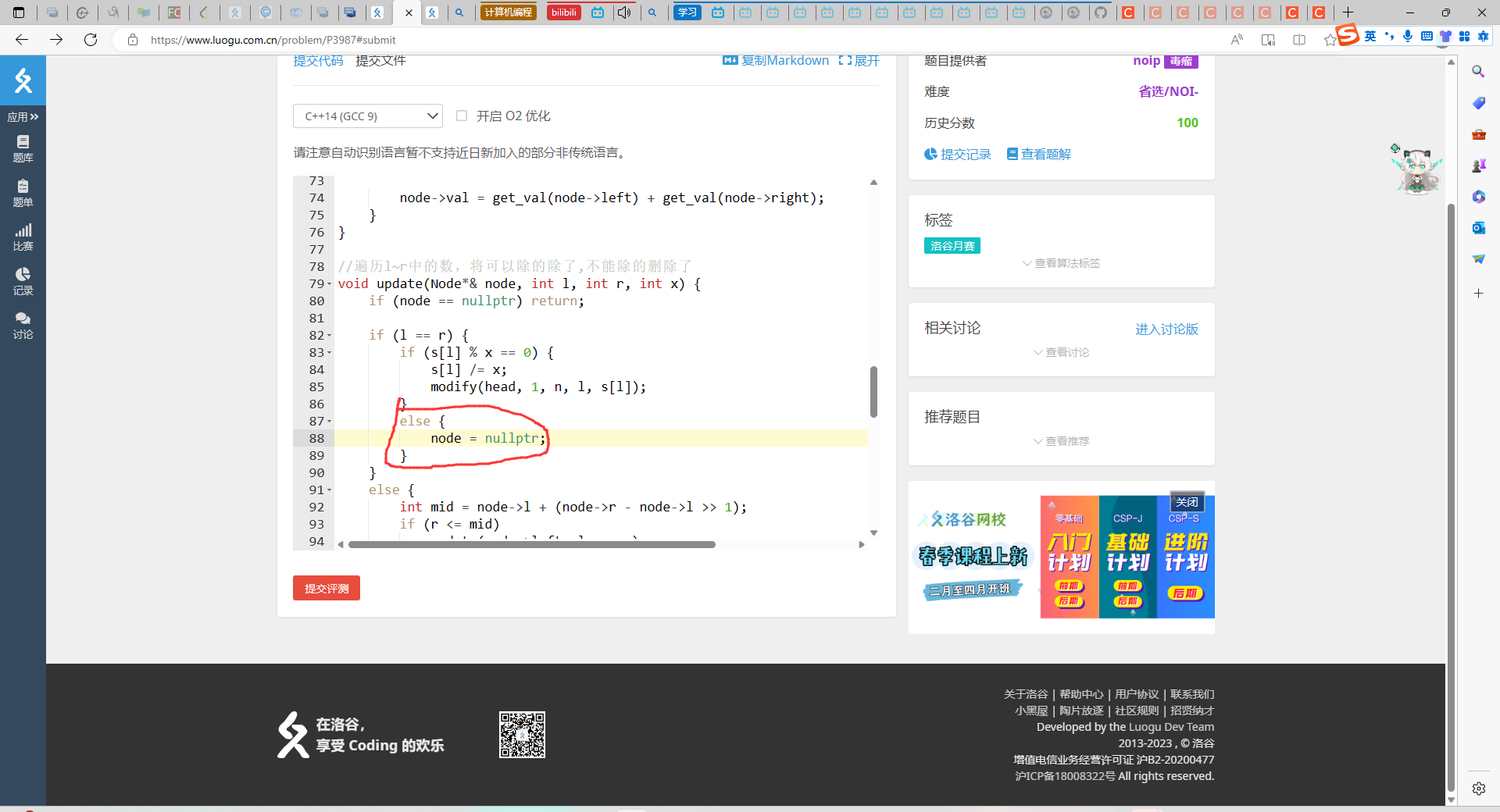这里s[l] % x != 0。那后面应该没有用了吧？为什么= nullptr; 后原来对的会变成错的？
加上前 2~Y@VX081N02%I_JTDSUWLM.png

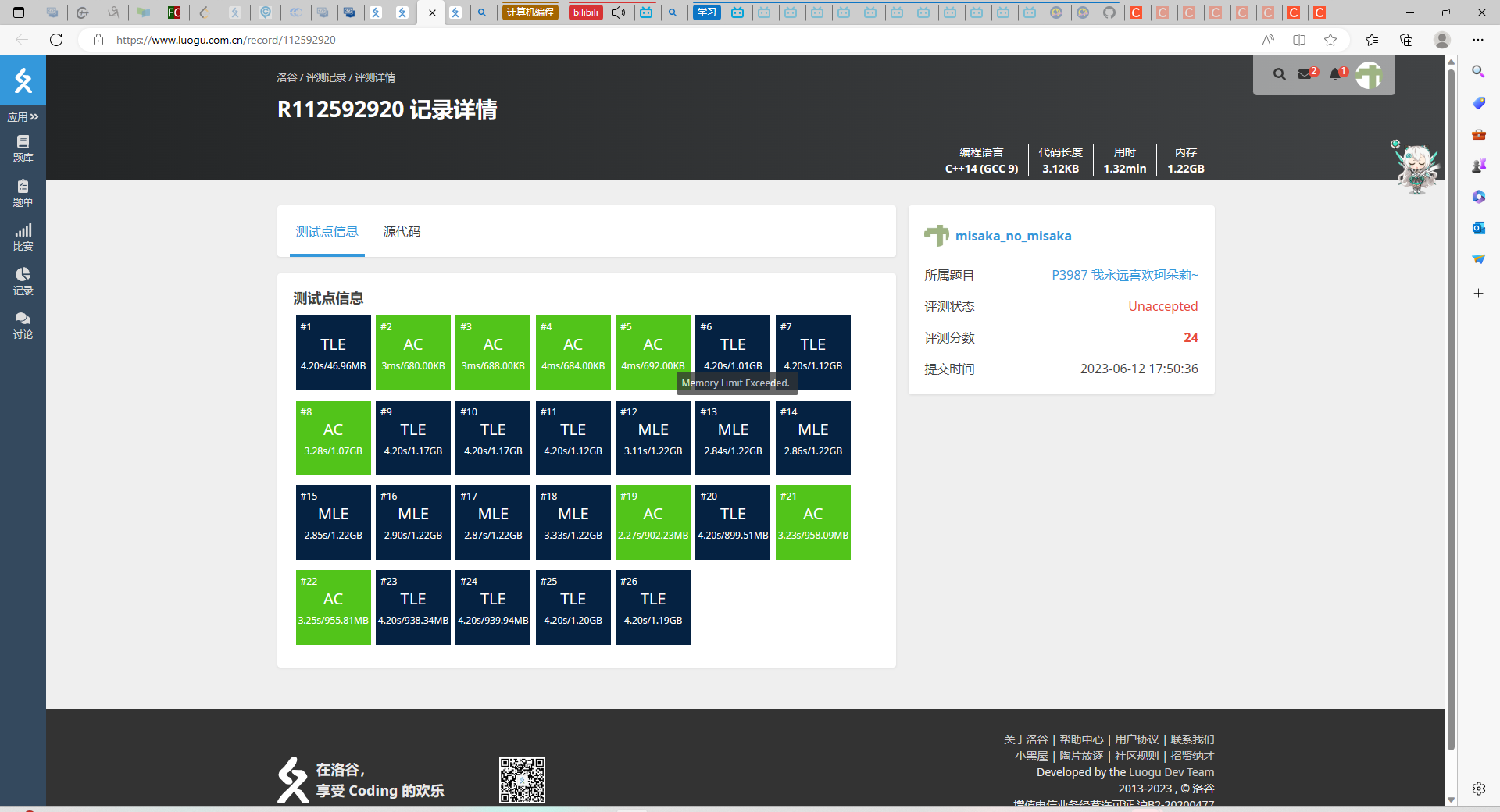
加上后

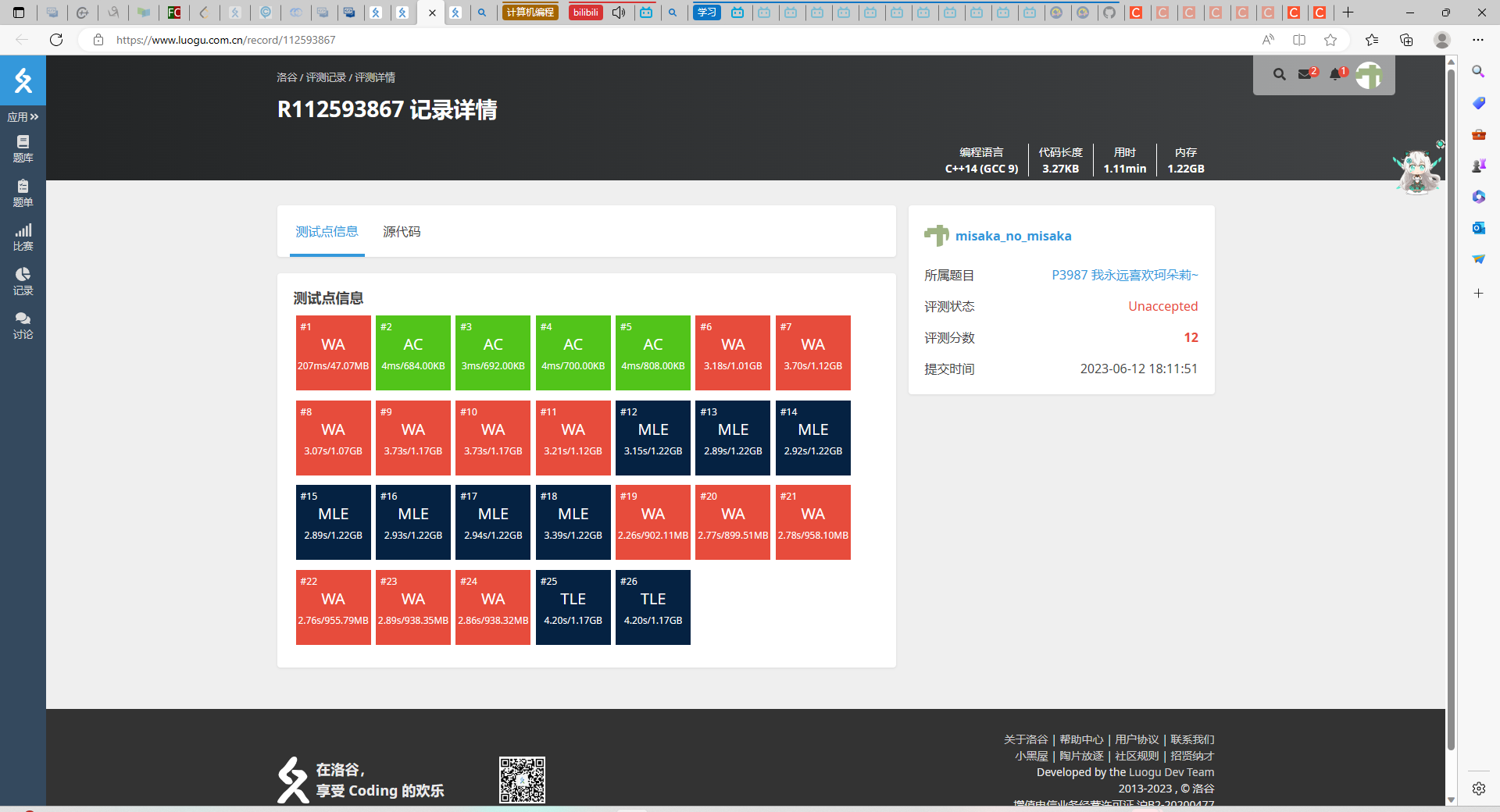
#include <iostream>
#include <vector>

using namespace std;

const int MAX = 5e5 + 5;

struct Node {
    int l, r;
    long long val;
    Node* left, * right;

    Node(long long val, int l, int r) : val(val), l(l), r(r), left(nullptr), right(nullptr) {}
};

int n, m;
long long s[MAX];
Node* head = nullptr;
Node* f[MAX] = { nullptr };

long long get_val(Node* node) {
    if (node == nullptr)
        return 0;
    return node->val;
}

//查询l到r的和
long long query(Node* node, int l, int r) {
    if (node == nullptr) 
        return 0;
    if (l == node->l && r == node->r) 
        return node->val;

    int mid = node->l + (node->r - node->l >> 1);
    if (r <= mid)
        return query(node->left, l, r);
    else if (mid < l)
        return query(node->right, l, r);
    else
        return query(node->left, l, mid) + query(node->right, mid + 1, r);
}

//修改v处的值为x
void modify(Node*& node, int l, int r, int v, long long x) {
    if (node == nullptr) 
        node = new Node(0, l, r);
    if (node->l == node->r) {
        node->val = x;
    }
    else {
        int mid = node->l + (node->r - node->l >> 1);
        if (v > mid)
            modify(node->right, mid + 1, r, v, x);
        else
            modify(node->left, l, mid, v, x);

        node->val = get_val(node->left) + get_val(node->right);
    }
}

//根据s数组构建一颗树
void create(Node*& node, int l, int r) {
    if (node == nullptr) {
        node = new Node(0, l, r);
    }
    if (l == r) {
        node->val = s[l];
    }
    else {
        int mid = node->l + (node->r - node->l >> 1);
        create(node->left, l, mid);
        create(node->right, mid + 1, r);

        node->val = get_val(node->left) + get_val(node->right);
    }
}

//遍历l~r中的数，将可以除的除了,不能除的删除了
void update(Node*& node, int l, int r, int x) {
    if (node == nullptr) return;

    if (l == r) {
        if (s[l] % x == 0) {
            s[l] /= x;
            modify(head, 1, n, l, s[l]);
        }
        else {
            node = nullptr; //这里不加，大部分超时，加了，答案错误
        }
    }
    else {
        int mid = node->l + (node->r - node->l >> 1);
        if (r <= mid)
            update(node->left, l, r, x);
        else if (mid < l)
            update(node->right, l, r, x);
        else
            update(node->left, l, mid, x), update(node->right, mid + 1, r, x);

        node->val = get_val(node->left) + get_val(node->right);

        if (node->val == 0) {
            node = nullptr;
        }
    }
}

int main() {
    ios_base::sync_with_stdio(0);   //把cin和scnf分割开,加快速度
    cin.tie(0); //解除cin与cout的绑定

    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        for (int j = 1; j * j <= s[i]; j++) {
            if (s[i] % j == 0) {
                modify(f[j], 1, n, i, 1);
                if (j * j != s[i])
                    modify(f[s[i] / j], 1, n, i, 1);
            }
        }
    }

    create(head, 1, n);

    for (int i = 0; i < m; i++) {
        int num, l, r, x;
        cin >> num >> l >> r;
        if (num == 1) {
            cin >> x;
            if (x == 1) continue;
            update(f[x], l, r, x);
        }
        else {
            cout << query(head, l, r) << '\n';
        }
    }

    return 0;
}

最佳答案

月排行榜 / 总排行榜

不二如是

2023-6-12 18:19:40

s[l] % x != 0表示该位置的数不能整除x,所以后续的查询和修改都不会用到这个节点了。

但是如果直接node = nullptr删除这个节点,之前通过这个节点存储的信息也会丢失。

举个例子:
原数组:1 2 3 4
构建的线段树:

1-4 (1+2+3+4=10)
/ \
1-2 (1+2=3) 3-4 (3+4=7)

现在有修改操作:2-3 3 (把区间2-3的数除以3)
线段树变成:

1-4 (1+1+1+4=7)
/ \
1-2 (1+1=2) 3-4 (3+4=7)

此时再有查询操作1-4,应该返回7。

而如果直接删除节点3-4,则:

1-4
/
1-2 (1+1=2)

则查询1-4会返回2,与预期不符。

所以,采用if检查判断是否需要删除节点,如果需要删除再设置为nullptr的做法是正确的。既避免了直接删除节点导致信息丢失的情况,也删除了不再需要的节点。

希望通过这个例子能够理解为什么要加if判断,以及不加if判断会产生什么错误。如果还有不清楚的地方,欢迎再提问。

跳转到最佳答案楼层

不二如是 · 发表于 2023-6-12 18:19:40