|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x

在线学习:
竹虫与橡皮筋悖论("Antonarubberrope"paradox),也称为“蚂蚁和橡皮筋问题”,是一个经典的数学悖论,涉及到无限序列的求和问题。
这个问题通常是这样描述的:
想象一只蚂蚁开始在一个初始长度为1米的橡皮筋的一端爬行,蚂蚁的速度是每秒1厘米。同时,橡皮筋均匀地以每秒1米的速度拉长。问题是,蚂蚁是否最终会到达橡皮筋的另一端?
直观上,似乎随着橡皮筋的不断拉长,蚂蚁永远无法达到终点。然而,通过数学分析可以证明蚂蚁最终会到达橡皮筋的另一端,尽管这需要无限长的时间。这个悖论揭示了对无限过程的直觉理解可能存在的误区。
数学解释
在解决这个问题时,可以考虑橡皮筋的拉伸和蚂蚁的爬行对蚂蚁在橡皮筋上位置的影响。
如果将时间划分为无限小的间隔,每一个时间间隔内,蚂蚁前进的相对位置是其当前位置加上其前进的距离,而橡皮筋的长度也相应地增加。
具体来说,如果在某个时间点t蚂蚁在橡皮筋上的位置比例是x(t)(例如,如果蚂蚁位于橡皮筋的中点,x(t)就是0.5)。
那么在下一个时间点,这个位置比例会是:
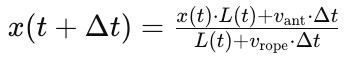
其中,L(t)是时间t时橡皮筋的长度,vant是蚂蚁的速度,是橡皮筋的拉长速度,而Δt是时间间隔。
通过将这个比例随时间的变化积分,我们可以看到蚂蚁的位置比例x(t)实际上会逐渐接近1,即橡皮筋的另一端。
结论
竹虫与橡皮筋悖论提供了一个对无限小分析和极限理论直观而深刻的理解,展示了数学在解释看似悖论的现象中的力量。
尽管从物理现实的角度,蚂蚁在达到终点前橡皮筋可能已经无限长了。
但从数学上讲,蚂蚁确实 |
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)