|
|
马上注册，结交更多好友，享用更多功能^_^
您需要 登录 才可以下载或查看，没有账号？立即注册
x
用一节课的时间，提高生活幸福感
------小甲鱼
欢乐与傻笑并存
智慧与邪恶同在
笔记内涵------
二叉树的定义
世上树有万千种，唯有二叉课上讲。
这里的“二叉”是二叉树，因为二叉树使用的范围最广，最具有代表意义，因此我们重点讨论二叉树。
定义：
二叉树（Binary Tree）是n（n>=0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
这个定义显然是递归形式的，所以咱看上去有点晕。
因为自古有云：
二叉树的特点
每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。
注意：
不是都需要两棵子树，而是最多可以是两棵，没有子树或者有一棵子树也都是可以的。
左子树和右子树是有顺序的，次序不能颠倒。
即使树中某结点只有一棵子树，也要区分它是左子树还是右子树，下面是完全不同的二叉树：
五种基本形态
空二叉树
只有一个根结点
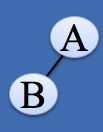根结点只有左子树
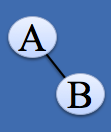根结点只有右子树
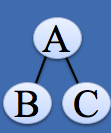根结点既有左子树又有右子树
很二的二叉树
为什么这么说呢？
因为若只从形态上来考虑，拥有三个结点的普通树只有两种情况：
但对于很二的二叉树来说，由于要区分左右，所以就演变成五种形态：
特殊二叉树-斜树
因为他很二，所以他也很特殊。
接下来再介绍一下一些特殊的二叉树。
虽然暂时你可能不能理解它们的用处，但我们有必要先了解一下。
斜树：
特殊二叉树-满二叉树
坡坡有云：
“人有悲欢离合，月有阴晴圆缺，此事古难全。但愿人长久，千里共长娟。”
意思就是说：
但是对于二叉树来说，是否存在完美呢？
有滴，那就是满二叉树啦。
满二叉树 VS 完全二叉树
在一棵二叉树中，如果所有分支结点都存在左子树和右子树。
并且所有叶子都在同一层上，这样的二叉树称为满二叉树。
例如：
满二叉树的特点有：
◊叶子只能出现在最下一层。
◊非叶子结点的度一定是2。
◊在同样深度的二叉树中，满二叉树的结点个数一定最多，同时叶子也是最多。
满二叉树和完全二叉树历年都是一个重大考点，因为考生很容易混淆两者。
完全二叉树定义：
对一棵具有n个结点的二叉树按层序编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同
例如：
完全二叉树的特点有：
◊叶子结点只能出现在最下两层。
◊最下层的叶子一定集中在左部连续位置。
◊倒数第二层，若有叶子结点，一定都在右部连续位置。
◊如果结点度为1，则该结点只有左孩子。
◊同样结点树的二叉树，完全二叉树的深度最小。
二者考试重点：
满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树。
以下这些都不是完全二叉树：
课后作业
二叉树性质：
这位鱼油，如果喜欢本系列笔记，请订阅 专辑☞（ 传送门）（ 不喜欢更要订阅 ） |
|
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2017-11-3 14:03:24
置顶卡
千斤顶
显身卡
发表于 2018-5-2 19:32:27
发表于 2019-2-13 11:02:14
