|
|
马上注册，结交更多好友，享用更多功能^_^
您需要 登录 才可以下载或查看，没有账号？立即注册
x
本帖最后由 小甲鱼的二师兄 于 2024-2-11 05:13 编辑
在股票和基金市场中，不确定性是唯一可以确定的事情！
技术和统计学可以为投资者提供重要的见解，帮助他们更好地理解市场动态。
特别地，蒙特卡罗模拟作为一种强大的统计技术，可以模拟股票市场的潜在未来行为。
这篇文章将详细介绍如何使用 Python 和统计学原理来实施蒙特卡罗模拟，并分析股票市场。
蒙特卡罗模拟简介
蒙特卡罗是一种计算数学的方法，通过重复随机抽样来获得数值结果。
这种方法得名于摩纳哥的蒙特卡罗赌场，因为赌博的本质涉及随机性与概率，与蒙特卡罗模拟中的随机抽样过程类似。
蒙特卡罗模拟（Monte Carlo Simulation）是一种概率模型，用于预测可能的结果，其核心思想是通过重复随机抽样来模拟一个或多个随机变量的概率分布。
它特别适用于系统或过程中存在不确定性的情况，可以帮助研究者和决策者评估风险和不确定性，并做出更好的决策。
在金融领域，蒙特卡罗模拟被用于模拟资产价格的未来走势、评估风险、定价期权以及进行资产组合优化等多种应用。
蒙特卡罗模拟实现
下面我们以苹果公司（AAPL）自 2010-01-01 到 2024-02-10 的数据为例：
apple_stock_data.zip
(99.35 KB, 下载次数: 11, 售价: 10 鱼币)
演示如何基于股票的历史日收益率来计算其均值和标准差，然后使用这些参数生成正态分布的随机数，模拟股票价格的未来路径。
下面我们的 DEMO 将模拟该股票未来 365 天的 10000 种可能性，并计算出每天所有模拟的中间值，最后通过 matplotlib 将这些数据可视化。
- import pandas as pd
- import numpy as np
- import matplotlib.pyplot as plt
- def monte_carlo_simulation(data, simulations, days):
- prices = data["Adj Close"]
-
- # 计算日收益率
- daily_returns = prices.pct_change().dropna()
- # 计算日收益率的均值和标准差
- mean_return = daily_returns.mean()
- std_dev = daily_returns.std()
- # 根据正态分布生成随机数
- simulations = np.random.normal(loc=mean_return, scale=std_dev, size=(simulations, days))
- # 计算模拟价格
- simulated_prices = prices.iloc[-1] * (1 + simulations).cumprod(axis=1)
- # 获取每天所有模拟的中间值
- median_simulated_prices = np.median(simulated_prices, axis=0)
- # 可视化结果
- plt.figure(figsize=(10, 6))
- plt.plot(simulated_prices.T, alpha=0.1) # 模拟的价格路径
- plt.plot(median_simulated_prices, color='red', linewidth=1) # 中间值价格路径
- plt.title('Monte Carlo Simulation for APLL by FishC')
- plt.xlabel('Days')
- plt.ylabel('Price')
- plt.show()
- if __name__ == "__main__":
- # 获取历史数据
- data = pd.read_csv("apple_stock_data.csv")
- # 使用蒙特卡罗
- monte_carlo_simulation(data, 1000, 365)
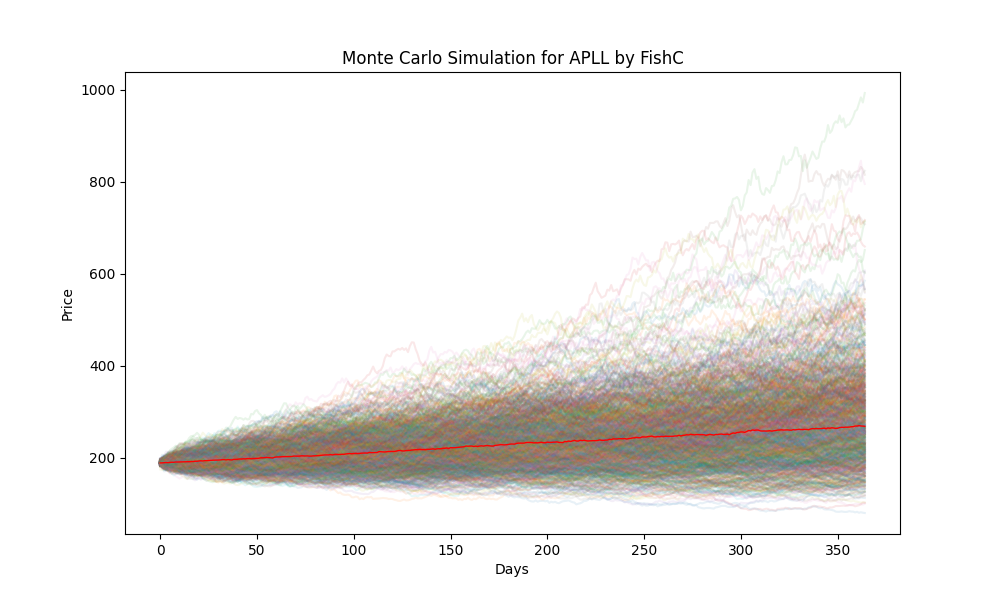
实现效果如下：
|
|
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
狗仔卡
发表于 2024-2-10 16:38:33
置顶卡
千斤顶
显身卡
发表于 2024-2-11 09:47:23
发表于 2024-2-11 09:52:59
发表于 2024-2-11 11:00:18
楼主
众所周知，A 股是稳如老狗的……不过通过蒙特卡洛模拟分析可以帮你排除掉很多坑，如果看到预期是下行的，直接不用看，肯定是废的~