|
|
马上注册,结交更多好友,享用更多功能^_^
您需要 登录 才可以下载或查看,没有账号?立即注册
x
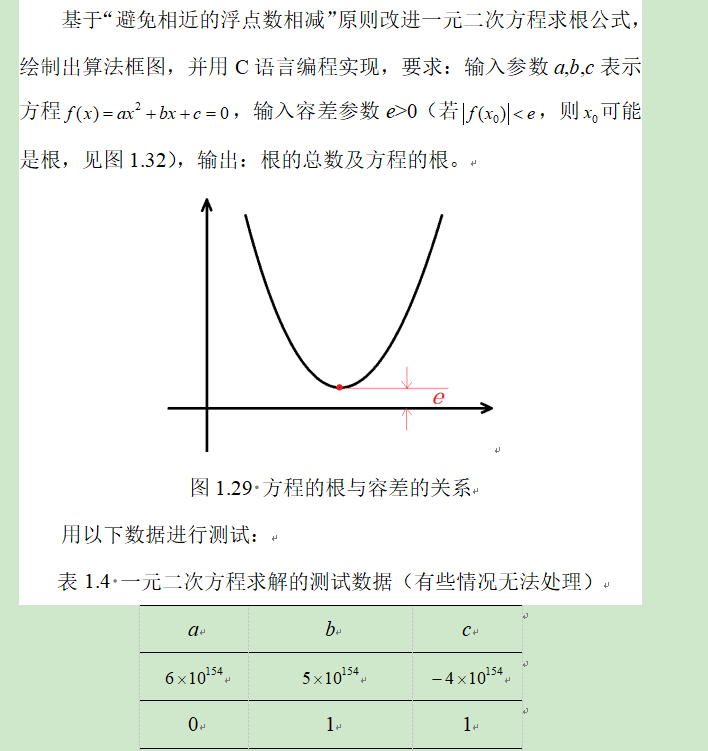
具体问题描述如图。
目前代码如下。
用的是c语言。
#include <stdio.h>
#include "math.h"
int main()
{
double a, b, c, d, x1, x2,e = 1e-10 ;
printf("请输入a,b,c,代入f(x)=ax2+bx+c中:");
scanf("%lf%lf%lf",&a,&b,&c);
if
printf("%lf",b);
if(fabs(a)<e){
x1 = -c/b;
printf("方程有一个根,为%lf",x1);
}
else{
d = b*b-4*a*c;
if(d<e){
printf("该方程无解。");
}
else if(fabs(d)<e){
x1 = x2 = -b/(2*a);
printf("该方程有两个相等的解x1=x2=%lf",x1,x2);
}
else{
d = sqrt(d) ;
x1 = (-b+d)/(2*a) ;
x2 = (-b-d)/(2*a) ;
printf("该方程有两个解,x1=%lf,x2=%lf",x1,x2);
}
}
return 0;
}
鱼油代码中的逻辑是正确的方向,但是有一些部分似乎是不完整滴~
特别是:
同时需要处理判断式 fabs(d) < e 的情况,这里用于判断判别式是否接近于0,意味着两个根相等。
去修正这些地方:
- 1. 在进行 fabs(a) < e 判断时,应该考虑 b 也接近于0的情况,否则会导致除以 0 的情况。
- 2. 在判断 d < e 时,应该比较 d < 0 来确定方程是否无解,因为当判别式小于0时,方程没有实数解。
- 3. 在比较 fabs(d) < e 时,应该确认 d 是否接近0来判断方程是否有两个相等的实数解。
以下是修正后的代码段,以更正这些问题:
- //... 省略了部分代码
- if(fabs(a) < e){
- if(fabs(b) < e) {
- printf("该方程无解。");
- } else {
- x1 = -c/b;
- printf("方程有一个根,为%lf", x1);
- }
- } else {
- d = b*b - 4*a*c;
- if(d < -e){
- printf("该方程无解。");
- } else if(fabs(d) < e){
- x1 = -b / (2*a);
- printf("该方程有两个相等的解x1=x2=%lf", x1);
- } else {
- d = sqrt(d);
- x1 = (-b + d) / (2*a);
- x2 = (-b - d) / (2*a);
- printf("该方程有两个解,x1=%lf,x2=%lf", x1, x2);
- }
- }
拿走不谢
|
-
|
 ( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)
( 粤ICP备18085999号-1 | 粤公网安备 44051102000585号)